题目内容
 如图,是一个防盗窗棂的示意图,如果测得∠1=60°,∠2=60°,∠3=60°,能否断定AB∥CD,已知条件够不够?如不够,需要再补充一个什么条件?
如图,是一个防盗窗棂的示意图,如果测得∠1=60°,∠2=60°,∠3=60°,能否断定AB∥CD,已知条件够不够?如不够,需要再补充一个什么条件?考点:平行线的判定
专题:常规题型
分析:根据平行线的判定方法由∠1=60°,∠2=60°,∠3=60°不能断定AB∥CD,当补充BA=BC时,则∠BAC=∠3=60°=∠2,于是可根据内错角相等,两直线平行得到AB∥CD.
解答:解:不能判断AB∥CD,可以补充BA=BC.
∵BA=BC,
∴∠BAC=∠3=60°,
而∠2=60°,
∴∠BAC=∠2,
∴AB∥CD.
∵BA=BC,
∴∠BAC=∠3=60°,
而∠2=60°,
∴∠BAC=∠2,
∴AB∥CD.
点评:本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
 如图所给几何体的俯视图是( )
如图所给几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
要使多项式(2k-3)x2y+3x-x2y-5y+1中不含x2y的项,则k的值应是( )
A、
| ||
| B、2 | ||
| C、1 | ||
| D、-1 |
 看图填空:
看图填空: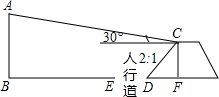 城市规划期间,欲拆除一电线杆AB(如图),已知距电线杆AB水平距离14m的D处有一大坝,背水坝CD的坡度i=2:1,坝高CF为2m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道.求BF长.
城市规划期间,欲拆除一电线杆AB(如图),已知距电线杆AB水平距离14m的D处有一大坝,背水坝CD的坡度i=2:1,坝高CF为2m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道.求BF长.