题目内容
 在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C(-1,0),如图所示,过点B作BD⊥x轴,垂足为D,且点B横坐标为-3
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C(-1,0),如图所示,过点B作BD⊥x轴,垂足为D,且点B横坐标为-3(1)求证:△BDC≌△C0A;
(2)求BC所在直线的函数解析式;
(3)若点P(x,y)是在轴下方的直线BC上的一动点,当点P运动过程中,试写出△POC的面积S与x的函数关系式.
考点:一次函数综合题
专题:
分析:(1)根据∠BCD+∠ACO=90°,∠ACO+∠OAC=90°,可得∠BCD=∠OAC,然后利用AAS可证明△BDC≌△COA;
(2)分别求出点B和点C的坐标,然后设出函数关系,代入求出BC所在直线的函数解析式;
(3)根据S△POC=
OC•|yP|即可求得△POC的面积S与x的函数关系式.
(2)分别求出点B和点C的坐标,然后设出函数关系,代入求出BC所在直线的函数解析式;
(3)根据S△POC=
| 1 |
| 2 |
解答:(1)证明:∵∠BCD+∠ACO=90°,∠ACO+∠OAC=90°,
∴∠BCD=∠OAC,
∵△ABC为等腰直角三角形,
∴BC=AC,
在△BDC和△COA中,
∴△BDC≌△COA(AAS);
(2)解:∵C点坐标为(-1,0),
∴BD=CO=1,
∵B点横坐标为-3,
∴B点坐标为(-3,1),
设BC所在直线的函数关系式为y=kx+b,
∴
,
解得:
,
∴BC所在直线的解析式为y=-
x-
;
(3)解:∵点P(x,y)是在轴下方的直线BC上的一动点,
∴y=-
x-
;
∴S△POC=
OC•|yP|=
×1×(
x+
)=
x+
,(x>-1);
故△POC的面积S与x的函数关系式为:S=
x+
,(x>-1);

∴∠BCD=∠OAC,
∵△ABC为等腰直角三角形,
∴BC=AC,
在△BDC和△COA中,
∴△BDC≌△COA(AAS);
(2)解:∵C点坐标为(-1,0),
∴BD=CO=1,
∵B点横坐标为-3,
∴B点坐标为(-3,1),
设BC所在直线的函数关系式为y=kx+b,
∴
|
解得:
|
∴BC所在直线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
(3)解:∵点P(x,y)是在轴下方的直线BC上的一动点,
∴y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴S△POC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
故△POC的面积S与x的函数关系式为:S=
| 1 |
| 4 |
| 1 |
| 4 |

点评:本题主要考查全等三角形的判定与性质,待定系数法求出抛物线的解析式,求三角形的面积等,根据解析式求点的坐标,关键在于(1)推出∠BCD=∠OAC,(2)根据(1)的结论推出B点的坐标.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
下列方程变形一定成立的是( )
A、如果S=
| ||||
B、如果
| ||||
| C、如果x-3=2x-3,那么x=0 | ||||
| D、如果mx=my,那么x=y |
 如图,借助三角尺画出15°,75°的角,用一副三角尺,你还能画出一个
如图,借助三角尺画出15°,75°的角,用一副三角尺,你还能画出一个

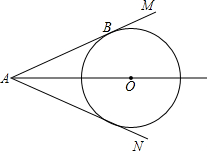 已知,如图,点O是的角∠MAN平分线上任意一点,以点O为圆心的圆切AM于点B.
已知,如图,点O是的角∠MAN平分线上任意一点,以点O为圆心的圆切AM于点B.