题目内容
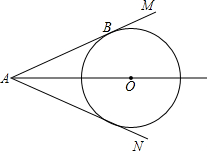 已知,如图,点O是的角∠MAN平分线上任意一点,以点O为圆心的圆切AM于点B.
已知,如图,点O是的角∠MAN平分线上任意一点,以点O为圆心的圆切AM于点B.(1)求证:直线AN是⊙O的切线;
(2)在(1)的条件下,若∠MAN=60°,且AO=2cm,求两切点之间的弧长.
考点:切线的判定,弧长的计算
专题:
分析:(1)连接OB,作OC⊥AN于C,根据切线性质推出OB⊥AM,根据角平分线性质得出OC=OB,根据切线的判定推出即可;
(2)先求得∠BOC=120°,根据30°角所对的直角边等于斜边的一半求得半径,然后根据弧长公式即可求得.
(2)先求得∠BOC=120°,根据30°角所对的直角边等于斜边的一半求得半径,然后根据弧长公式即可求得.
解答: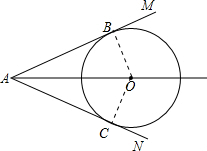 (1)证明:连接OB,作OC⊥AN于C,
(1)证明:连接OB,作OC⊥AN于C,
∵⊙O切AM于B,
∴OB⊥AM,
又∵AO平分∠MPN,OC⊥AN,
∴OC=OB,
∴直线AN是⊙O的切线.
(2)解∵直线AN,AM是⊙O的切线,
∴∠MAO=
∠MAN=
×60°=30°,
∵OC⊥AN,OB⊥AM,
∴∠ABO=∠ACO=90°,
∴∠BOC=360°-∠MAN-∠ABO-∠ACO=360°-60°-90°-90°=120°,
在RT△ABO中,∠MAO=30°,AO=2cm,
∴OB=
AO=
×2=1cm,
∴劣弧BC的长为
=
π,
同理:优弧BC的长为
=
π,
∴两切点之间的弧长为
π或
π.
 (1)证明:连接OB,作OC⊥AN于C,
(1)证明:连接OB,作OC⊥AN于C,∵⊙O切AM于B,
∴OB⊥AM,
又∵AO平分∠MPN,OC⊥AN,
∴OC=OB,
∴直线AN是⊙O的切线.
(2)解∵直线AN,AM是⊙O的切线,
∴∠MAO=
| 1 |
| 2 |
| 1 |
| 2 |
∵OC⊥AN,OB⊥AM,
∴∠ABO=∠ACO=90°,
∴∠BOC=360°-∠MAN-∠ABO-∠ACO=360°-60°-90°-90°=120°,
在RT△ABO中,∠MAO=30°,AO=2cm,
∴OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴劣弧BC的长为
| 120π×1 |
| 180 |
| 2 |
| 3 |
同理:优弧BC的长为
| 240π×1 |
| 180 |
| 4 |
| 3 |
∴两切点之间的弧长为
| 2 |
| 3 |
| 4 |
| 3 |
点评:本题考查了切线的判定和性质,含有30°角的直角三角形的性质,弧长的计算等,作出OC⊥AN是解题的关键.

练习册系列答案
相关题目
 如图所示的正方体沿某些棱展开后,能得到的平面图形是( )
如图所示的正方体沿某些棱展开后,能得到的平面图形是( )A、 |
B、 |
C、 |
D、 |
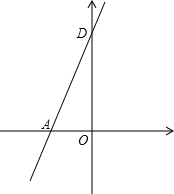 如图,已知直线y=2x+6与x轴、y轴分别交于A、D两点,抛物线y=ax2+bx+2(a≠0)经过点A和点B(1,0).
如图,已知直线y=2x+6与x轴、y轴分别交于A、D两点,抛物线y=ax2+bx+2(a≠0)经过点A和点B(1,0). 在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C(-1,0),如图所示,过点B作BD⊥x轴,垂足为D,且点B横坐标为-3
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C(-1,0),如图所示,过点B作BD⊥x轴,垂足为D,且点B横坐标为-3 (Ⅰ)一个三角形的内心是这个三角形的
(Ⅰ)一个三角形的内心是这个三角形的