题目内容
20. 如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( )
如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由AD⊥BC可得出∠ADC=90°,结合∠BAC=90°可得出∠ABC和∠DAC均与∠ACB互余,由此得出∠ABC=∠DAC;由AB∥DE可得出∠ABC=∠EDC,结合前面结论即可得出∠EDC=∠DAC,故可寻找出2个与∠DAC相等的角.
解答 解:∵∠BAC=90°,
∴∠ABC+∠ACB=180°-∠BAC=90°,
又∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC+∠ACD=90°,
∴∠ABC=∠DAC.
∵AB∥DE,
∴∠ABC=∠EDC,
又∵∠ABC=∠DAC,
∴∠EDC=∠ABC=∠DAC.
∴有两个与∠DAC相等的角.
故选B.
点评 本题考查了平行线的性质以及直角三角形的性质,解题的关键是利用互余和平行找出∠EDC=∠ABC=∠DAC.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等的角,再结合直角三角形的性质利用互余得出结论.

练习册系列答案
相关题目
11.下列各式中一定是二次根式的是( )
| A. | $\sqrt{{x}^{2}+1}$ | B. | $\sqrt{x}$ | C. | $\root{3}{27}$ | D. | $\sqrt{{x}^{2}-2}$ |
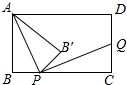 如图,在矩形ABCD中,AB=6,BC=8,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PAB沿直线PA折叠,使点B落到点B′处;过点P作∠CPB′的角平分线交CD于点Q.设BP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,在矩形ABCD中,AB=6,BC=8,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PAB沿直线PA折叠,使点B落到点B′处;过点P作∠CPB′的角平分线交CD于点Q.设BP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )