题目内容
15.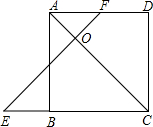 如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.
如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.
分析 连接AE、CF,先由SAS证明△ABE≌△CDF,得出AE=CF,∠AEB=∠CFD,再证明△AEC≌△FCE,得出∠ACE=∠FEC=45°,OE=OC,因此∠EOC=90°,即可得出结论.
解答 证明:连接AE、CF,如图所示: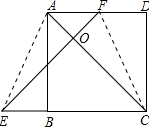 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=CD,AD∥BC,∠ABC=∠ADC=90°,
∴∠AEB=90°,∠ECF=∠CFD,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{AB=CD}&{\;}\\{∠ABE=∠CDF=90°}&{\;}\\{BE=DF}&{\;}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD,
∴∠AEB=∠ECF,
在△AEC和△FCE中,
$\left\{\begin{array}{l}{AE=CF}&{\;}\\{∠AEB=∠ECF}&{\;}\\{EC=CE}&{\;}\end{array}\right.$,
∴△AEC≌△FCE(SAS),
∴∠ACE=∠FEC=45°,
∴OE=OC,∠EOC=90°,
∴△OEC为等腰直角三角形.
点评 本题考查了正方形的性质、全等三角形的判定与性质以及等腰直角三角形的判定;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
10.计算($\frac{1}{2}$x)3÷(-$\frac{1}{2}$x)2的结果是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$x | C. | -$\frac{{x}^{2}}{2}$ | D. | -$\frac{1}{2}$x |
 时钟的分针每分钟转过的角度是6°,时针每分钟转过的角度是$\frac{1}{2}$°.今天我们数学考试的时间是13﹕00--14﹕30,在这一个半小时的时间内,时针与分针所夹的角将有几个时刻为36°?试分别求出这几个时刻.
时钟的分针每分钟转过的角度是6°,时针每分钟转过的角度是$\frac{1}{2}$°.今天我们数学考试的时间是13﹕00--14﹕30,在这一个半小时的时间内,时针与分针所夹的角将有几个时刻为36°?试分别求出这几个时刻. 已知直线AB:y=-3x+6与x轴、y轴分别交于点A、B,直线l经过点B,并且与直线AB垂直.
已知直线AB:y=-3x+6与x轴、y轴分别交于点A、B,直线l经过点B,并且与直线AB垂直. 如图△ABC中,D为BC边上一点,AB=15,BD=9,AD=12,AC=13,求△ABC的面积.
如图△ABC中,D为BC边上一点,AB=15,BD=9,AD=12,AC=13,求△ABC的面积.