题目内容
7.已知二次函数y=ax2+2ax-4(a≠0)的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12,求此二次函数的解析式.分析 设A(x1,0),B(x2,0),根据题意,得出x1+x2=-$\frac{2a}{a}$=-2,x1x2=$\frac{-4}{a}$=-$\frac{4}{a}$,C的坐标为(0,-4),然后根据三角形的面积得出$\frac{1}{2}×$|x1-x2|×4=12,进而得出(x1+x2)2-4x1x2=36,把x1+x2=-$\frac{2a}{a}$=-2,x1x2=$\frac{-4}{a}$=-$\frac{4}{a}$代入得到(-2)2-4×(-$\frac{4}{a}$)=36,解得a=$\frac{1}{2}$,从而求得解析式.
解答 解:设A(x1,0),B(x2,0),
根据题意,x1+x2=-$\frac{2a}{a}$=-2,x1x2=$\frac{-4}{a}$=-$\frac{4}{a}$,C的坐标为(0,-4),
∵△ABC的面积为12,
∴$\frac{1}{2}×$|x1-x2|×4=12,
∴(x1-x2)2=36,
∴(x1+x2)2-4x1x2=36,即(-2)2-4×(-$\frac{4}{a}$)=36,
解得a=$\frac{1}{2}$.
∴此二次函数的解析式为y=$\frac{1}{2}$x2+x-4.
点评 本题考查了待定系数法求二次函数的解析式,根据x轴的交点坐标和系数的关系得出x1+x2=-$\frac{2a}{a}$=-2,x1x2=$\frac{-4}{a}$=-$\frac{4}{a}$是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.计算a÷$\frac{a}{b}$•$\frac{1}{a}$的值是( )
| A. | 1 | B. | ab | C. | $\frac{b}{a}$ | D. | $\frac{a}{b}$ |
17.请你按下列程序进行计算,把答案填写在表格内,然后看看有什么规律,想想为什么会有这样的规律?

(1)填写表内的空格:
(2)你发现的规律是:(n2+n)÷n-n=1.

(1)填写表内的空格:
| 输入 n | 3 | 2 | -2 | $\frac{1}{3}$ | … |
| 输出答案y | 1 | 1 | 1 | 1 | … |
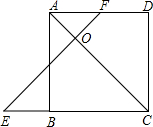 如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.
如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.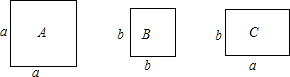 如图,正方形卡片A类、B类和长方形卡片C类各有若干张,如果要拼成一个长为a+2b,宽为a+b的大长方形,则需要A、B、C类卡片各多少张?
如图,正方形卡片A类、B类和长方形卡片C类各有若干张,如果要拼成一个长为a+2b,宽为a+b的大长方形,则需要A、B、C类卡片各多少张?