题目内容
5.化简:($\frac{{c}^{2}}{ab}$)2•($\frac{a}{bc}$)3÷($\frac{-c}{{a}^{2}b}$)3.分析 首先利用积的乘方进而化简,再利用分式的乘除运算法则化简即可.
解答 解:原式=($\frac{{c}^{2}}{ab}$)2•($\frac{a}{bc}$)3÷($\frac{-c}{{a}^{2}b}$)3
=$\frac{{c}^{4}}{{a}^{2}{b}^{2}}$×$\frac{{a}^{3}}{{b}^{3}{c}^{3}}$×$\frac{{a}^{6}{b}^{3}}{{-c}^{3}}$
=-$\frac{{a}^{7}}{{b}^{2}{c}^{2}}$.
点评 此题主要考查了分式的乘除运算法则,正确化简分式是解题关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
10.我县城市居民用电收费方式有以下两种:
估计小明家下月总用电量为200度,
(1)若其中峰时电量为50度,则小明家按照哪种方式付电费比较合适?能省多少元?
(2)请你帮小明计算,峰时电量为多少度时,两种方式所付的电费相等?
(3)到下月付费时,小明发现那月总用电量为200度,用峰谷电价付费方式比普通电价付费方式省了14元,求那月的峰时电量为多少度?
| 类别 | 普通电价 | 峰谷分时电价 | |
| 时间 | 每度0.52元 | 峰时(8;00-21:00) | 谷时(21:00-8:00) |
| 电价 | 每度0.55元 | 每度0.30元 | |
(1)若其中峰时电量为50度,则小明家按照哪种方式付电费比较合适?能省多少元?
(2)请你帮小明计算,峰时电量为多少度时,两种方式所付的电费相等?
(3)到下月付费时,小明发现那月总用电量为200度,用峰谷电价付费方式比普通电价付费方式省了14元,求那月的峰时电量为多少度?
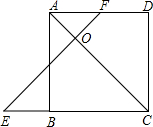 如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.
如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.