题目内容
4.已知x2-5x+1=0,求x4+$\frac{1}{{x}^{4}}$.分析 方程x2-5x+1=0两边同时除以x解得:x-5+$\frac{1}{x}$=0,即可求得x+$\frac{1}{x}$的值,然后两边平方即可求解x2+$\frac{1}{{x}^{2}}$的值,最后两边平方即可求解.
解答 解:方程x2-5x+1=0两边同时除以x解得:x-5+$\frac{1}{x}$=0,
则x+$\frac{1}{x}$=5,
两边平方得:x2+2+$\frac{1}{{x}^{2}}$=25,则x2+$\frac{1}{{x}^{2}}$=23,
两边再平方得:x4+$\frac{1}{{x}^{4}}$+2=529,
则x4+$\frac{1}{{x}^{4}}$=527.
点评 本题考查了完全平方公式的应用以及代数式的求值,理解x+$\frac{1}{x}$与x2+$\frac{1}{{x}^{2}}$之间的关系是关键.

练习册系列答案
相关题目
19.计算a÷$\frac{a}{b}$•$\frac{1}{a}$的值是( )
| A. | 1 | B. | ab | C. | $\frac{b}{a}$ | D. | $\frac{a}{b}$ |
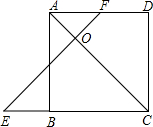 如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.
如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.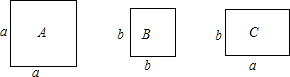 如图,正方形卡片A类、B类和长方形卡片C类各有若干张,如果要拼成一个长为a+2b,宽为a+b的大长方形,则需要A、B、C类卡片各多少张?
如图,正方形卡片A类、B类和长方形卡片C类各有若干张,如果要拼成一个长为a+2b,宽为a+b的大长方形,则需要A、B、C类卡片各多少张? 如图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请画出这个几何体的主视图和左视图.
如图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请画出这个几何体的主视图和左视图.