题目内容
5. 如图△ABC中,D为BC边上一点,AB=15,BD=9,AD=12,AC=13,求△ABC的面积.
如图△ABC中,D为BC边上一点,AB=15,BD=9,AD=12,AC=13,求△ABC的面积.
分析 已知△ABD三边的长度,运用勾股定理的逆定理首先证出AD⊥BC,然后在直角△ADC中,应用勾股定理求出CD,则BC=BD+DC,最后根据三角形的面积公式得出△ABC的面积.
解答 解:∵AD2+BD2=144+81=225,AB2=225,
∴AD2+BD2=AB2,
∴AD⊥BC(勾股定理的逆定理),
∴∠ADC=90°,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∴BC=CD+BD=5+9=14,
∴△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×14×12=84.
点评 本题考查了勾股定理的逆定理和勾股定理的运用,根据勾股定理的逆定理得出AD⊥BC是解题的关键.

练习册系列答案
相关题目
17.请你按下列程序进行计算,把答案填写在表格内,然后看看有什么规律,想想为什么会有这样的规律?

(1)填写表内的空格:
(2)你发现的规律是:(n2+n)÷n-n=1.

(1)填写表内的空格:
| 输入 n | 3 | 2 | -2 | $\frac{1}{3}$ | … |
| 输出答案y | 1 | 1 | 1 | 1 | … |
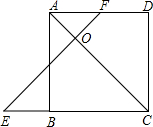 如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.
如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形. 如图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请画出这个几何体的主视图和左视图.
如图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请画出这个几何体的主视图和左视图.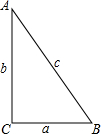 如图,在Rt△ABC中,两直角边长分别为a,b,斜边长为c,若Rt△ABC的面积为3,且a+b=5.则(1)ab=6;(2)c=$\sqrt{13}$.
如图,在Rt△ABC中,两直角边长分别为a,b,斜边长为c,若Rt△ABC的面积为3,且a+b=5.则(1)ab=6;(2)c=$\sqrt{13}$.