题目内容
求如图所示图形中阴影部分的面积.


考点:勾股定理
专题:
分析:如图,运用勾股定理求出每个图形中线段AB的长度,运用面积公式即可解决问题.
解答:
 解:如图(1),由勾股定理得:AB=
解:如图(1),由勾股定理得:AB=
=5,故阴影部分的面积
=52=25;
如图(2),同理可求:
AB=
=17,
故阴影部分的面积
=17×3=51;
如图(3),AB=
=4,
故阴影部分的面积
=22×π×
=2π.
 解:如图(1),由勾股定理得:AB=
解:如图(1),由勾股定理得:AB=| 132-122 |
=5,故阴影部分的面积
=52=25;
如图(2),同理可求:
AB=
| 152+82 |
故阴影部分的面积
=17×3=51;
如图(3),AB=
| 52-32 |
故阴影部分的面积
=22×π×
| 1 |
| 2 |
点评:该题主要考查了勾股定理及其应用问题;解题的关键是掌握勾股定理的本质内容,并能灵活运用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
下列命题中,真命题是( )
| A、如果x2=4,那么x=2 |
| B、对顶角相等 |
| C、相等的角是对顶角 |
| D、同旁内角互补 |
 AD是△ABC的高,下列能使△ABD≌ACD的条件是( )
AD是△ABC的高,下列能使△ABD≌ACD的条件是( )| A、BD=AC |
| B、∠B=45° |
| C、∠BAC=90° |
| D、AB=AC |
正方形具有而菱形不一定具有的性质是( )
| A、四条边相等 |
| B、对角线互相垂直平分 |
| C、对角线平分一组对角 |
| D、对角线相等 |
下列计算结果正确的是( )
| A、(x+y)2=x2+y2 |
| B、(x-y)2=x2-2xy-y2 |
| C、(x+2y)(x-2y)=x2-2y2 |
| D、(3x+y)2=9x2+6xy+y2 |
 如图,直线AB∥x轴,与抛物线y=ax2+bx+c交于点A(-2,-
如图,直线AB∥x轴,与抛物线y=ax2+bx+c交于点A(-2,- 如图,四边形ABCD中,AB=4,BC=13,CD=12,DA=3,∠A=90°,求四边形ABCD的面积.
如图,四边形ABCD中,AB=4,BC=13,CD=12,DA=3,∠A=90°,求四边形ABCD的面积.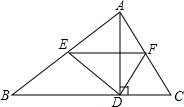 如图,在△ABC中,AD是高.
如图,在△ABC中,AD是高. 在△ABC中,AB=AC,点E、F分别在AB、AC上,AE=AF,BF与CE相交于点P.
在△ABC中,AB=AC,点E、F分别在AB、AC上,AE=AF,BF与CE相交于点P.