题目内容
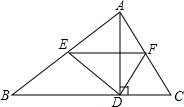 如图,在△ABC中,AD是高.
如图,在△ABC中,AD是高.(1)若AB=17,AC=10,BC=21,求AD.
(2)若E、F分别是AB、AC的中点,试说明EF垂直平分AD.
考点:勾股定理,全等三角形的判定与性质,线段垂直平分线的性质
专题:计算题
分析:(1)由AD为高,得到三角形ABD与三角形ACD都为直角三角形,利用勾股定理分别表示出AD2,设BD=x,列出关于x的方程,求出方程的解即可得到AD的长;
(2)利用直角三角形斜边上的中线等于斜边的一半得到AE=DE,AF=DF,以及EF为公共边,利用SSS得到三角形AEF与三角形EFD全等,利用全等三角形对应角相等得到∠AEF=∠DEF,再由AE=DE,即可得证.
(2)利用直角三角形斜边上的中线等于斜边的一半得到AE=DE,AF=DF,以及EF为公共边,利用SSS得到三角形AEF与三角形EFD全等,利用全等三角形对应角相等得到∠AEF=∠DEF,再由AE=DE,即可得证.
解答:
解:(1)∵AD是高,∴∠ADB=∠ADC=90°,
∴根据勾股定理得:AD2=AB2-BD2,AD2=AC2-CD2,
∴AB2-BD2=AC2-CD2,
设BD=x,则有172-x2=102-(21-x)2,
解得:x=15,
则AD=
=8;
(2)∵AD是高,E、F分别是AB、AC的中点,
∴AE=DE,AF=DF,
在△AEF和△DEF中,
,
∴△AEF≌△DEF(SSS),
∴∠AEF=∠DEF,
∵AE=DE,
∴EF垂直平分AD.
∴根据勾股定理得:AD2=AB2-BD2,AD2=AC2-CD2,
∴AB2-BD2=AC2-CD2,
设BD=x,则有172-x2=102-(21-x)2,
解得:x=15,
则AD=
| 172-152 |
(2)∵AD是高,E、F分别是AB、AC的中点,
∴AE=DE,AF=DF,
在△AEF和△DEF中,
|
∴△AEF≌△DEF(SSS),
∴∠AEF=∠DEF,
∵AE=DE,
∴EF垂直平分AD.
点评:此题考查了勾股定理,全等三角形的判定与性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
根据下列条件,能判定△ABC≌△MNP的是( )
| A、AB=MN,BC=NP,∠A=∠M |
| B、∠A=∠M,∠C=∠P,AC=NP |
| C、AB=MN,BC=NP,∠B=∠N |
| D、∠B=∠N,∠A=∠M,AC=NP |
 如图,已知在△ABC中,AB=12,AC=10,BC边上的高AD=8,求BC边的长.
如图,已知在△ABC中,AB=12,AC=10,BC边上的高AD=8,求BC边的长.
 如图,在Rt△ABC中,∠ACB=90°,M,N分别为AC,BC的中点,AN=5,BM=6,求AB的长.
如图,在Rt△ABC中,∠ACB=90°,M,N分别为AC,BC的中点,AN=5,BM=6,求AB的长.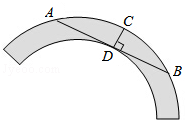 如图是一个古代车轮的碎片,形状为圆环的一部分,为求其外原半径,连接外圆上的两点A,B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=8cm,AB=48cm,则这个外圆半径为
如图是一个古代车轮的碎片,形状为圆环的一部分,为求其外原半径,连接外圆上的两点A,B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=8cm,AB=48cm,则这个外圆半径为