题目内容
 在△ABC中,AB=AC,点E、F分别在AB、AC上,AE=AF,BF与CE相交于点P.
在△ABC中,AB=AC,点E、F分别在AB、AC上,AE=AF,BF与CE相交于点P.(1)求证:PB=PC;
(2)你发现图中还有其他相等的线段是
考点:全等三角形的判定与性质
专题:
分析:(1)利用AAS得到三角形ABF与三角形ACE全等,利用全等三角形对应角相等得到∠ABF=∠ACE,由AB=AC,利用等边对等角得到一对角相等,利用等式的性质得到∠PBC=∠PCB,根据等角对等边即可得证;
(2)由(1)的结论得到BF=CE,PE=PF,BE=CF.
(2)由(1)的结论得到BF=CE,PE=PF,BE=CF.
解答:
(1)证明:在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠ABF=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB
∴∠ABC-∠ABF=∠ACB-∠ACE,
即∠PBC=∠PCB,
∴PB=PC.
(2)解:图中相等的线段为BF=CE,PE=PF,BE=CF.
|
∴△ABF≌△ACE(SAS),
∴∠ABF=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB
∴∠ABC-∠ABF=∠ACB-∠ACE,
即∠PBC=∠PCB,
∴PB=PC.
(2)解:图中相等的线段为BF=CE,PE=PF,BE=CF.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直线a,b相交于点O,若∠1等于50°,则∠2等于( )
如图,直线a,b相交于点O,若∠1等于50°,则∠2等于( )| A、40° | B、50° |
| C、130° | D、150° |
根据下列条件,能判定△ABC≌△MNP的是( )
| A、AB=MN,BC=NP,∠A=∠M |
| B、∠A=∠M,∠C=∠P,AC=NP |
| C、AB=MN,BC=NP,∠B=∠N |
| D、∠B=∠N,∠A=∠M,AC=NP |
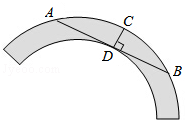 如图是一个古代车轮的碎片,形状为圆环的一部分,为求其外原半径,连接外圆上的两点A,B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=8cm,AB=48cm,则这个外圆半径为
如图是一个古代车轮的碎片,形状为圆环的一部分,为求其外原半径,连接外圆上的两点A,B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=8cm,AB=48cm,则这个外圆半径为若方程组
的解中,x的值比y的值大1,则k为( )
|
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |

 如图,已知长方形ABCD的两组对边分别与x轴,y轴平行,点A的坐标是(-2,2),△AOD的面积是7,作射线OA和OD.
如图,已知长方形ABCD的两组对边分别与x轴,y轴平行,点A的坐标是(-2,2),△AOD的面积是7,作射线OA和OD.