题目内容
 AD是△ABC的高,下列能使△ABD≌ACD的条件是( )
AD是△ABC的高,下列能使△ABD≌ACD的条件是( )| A、BD=AC |
| B、∠B=45° |
| C、∠BAC=90° |
| D、AB=AC |
考点:全等三角形的判定
专题:
分析:如图,对所给的四个选项逐一分析、判断,可以发现只有选项D符合题意,即可解决问题.
解答:
 解:能使△ABD≌ACD的条件是AB=AC;理由如下:
解:能使△ABD≌ACD的条件是AB=AC;理由如下:
∵AD是△ABC的高,
∴△ABD、△ACD均为直角三角形;
在Rt△ABD与Rt△ACD中,
,
∴Rt△ABD≌Rt△ACD(HL).
故选D.
 解:能使△ABD≌ACD的条件是AB=AC;理由如下:
解:能使△ABD≌ACD的条件是AB=AC;理由如下:∵AD是△ABC的高,
∴△ABD、△ACD均为直角三角形;
在Rt△ABD与Rt△ACD中,
|
∴Rt△ABD≌Rt△ACD(HL).
故选D.
点评:该题主要考查了全等三角形的判定定理及其应用问题;解题的关键是数形结合,准确找出图形中隐含的相等或全等关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 十一国庆期间,保龙仓超市对A,B两种型号的整理箱进行促销,促销价格如图所示,慧慧(其为会员)在该超市进行促销期间购买了2个A型号整理箱,3个B型号整理箱,若a=5,则慧慧总共花费( )
十一国庆期间,保龙仓超市对A,B两种型号的整理箱进行促销,促销价格如图所示,慧慧(其为会员)在该超市进行促销期间购买了2个A型号整理箱,3个B型号整理箱,若a=5,则慧慧总共花费( )| A、143.5元 |
| B、144.5元 |
| C、168.5元 |
| D、169.5元 |
 如图,直线a,b相交于点O,若∠1等于50°,则∠2等于( )
如图,直线a,b相交于点O,若∠1等于50°,则∠2等于( )| A、40° | B、50° |
| C、130° | D、150° |
 如图,已知在△ABC中,AB=12,AC=10,BC边上的高AD=8,求BC边的长.
如图,已知在△ABC中,AB=12,AC=10,BC边上的高AD=8,求BC边的长.

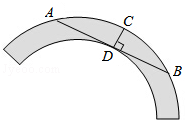 如图是一个古代车轮的碎片,形状为圆环的一部分,为求其外原半径,连接外圆上的两点A,B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=8cm,AB=48cm,则这个外圆半径为
如图是一个古代车轮的碎片,形状为圆环的一部分,为求其外原半径,连接外圆上的两点A,B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=8cm,AB=48cm,则这个外圆半径为