题目内容
如图1,线段AD、BC相交于点O,∠B=32°,∠D=38°
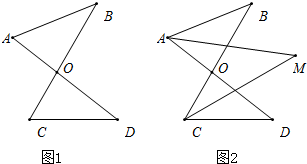
(1)若∠A=60°,求∠AOB和∠C的大小;
(2)如图2,若∠BAO、∠DCO的角平分线AM、CM相交于点M,求∠M的大小;
(3)若改变条件,设∠B=α,∠D=β,试用含α、β的代数式表示∠M的大小.

(1)若∠A=60°,求∠AOB和∠C的大小;
(2)如图2,若∠BAO、∠DCO的角平分线AM、CM相交于点M,求∠M的大小;
(3)若改变条件,设∠B=α,∠D=β,试用含α、β的代数式表示∠M的大小.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)在△AOB中利用三角形内角和定理可求得∠AOB,在△COD中可求得∠C;
(2)由条件可知∠M+∠BCM=∠B+∠BAM,再利用角平分线的定义可得到∠M=∠B+
(∠BAO-∠DCO),而在△AOB和△COD中可得∠B+∠BAO=∠D+∠DCO,可求得∠BAO-∠DCO的大小,从而可求得∠M;
(3)类似(2)可以找到∠B、∠D和∠M之间的关系.
(2)由条件可知∠M+∠BCM=∠B+∠BAM,再利用角平分线的定义可得到∠M=∠B+
| 1 |
| 2 |
(3)类似(2)可以找到∠B、∠D和∠M之间的关系.
解答:解:
(1)∵∠B=32°,∠A=60°,
∴∠AOB=180°-32°-60°=88°,
∵∠A+∠B=∠C+∠D,
∴∠C=∠A+∠B-∠D=60°+32°-38°=54°;
(2)∵∠M+∠BCM=∠B+∠BAM,
∴∠M=∠B+∠BAM-∠BCM,
∵AM、CM分别平分∠BAO、∠BCD,
∴∠BAM=
∠BAO,∠BCM=
∠DCO,
∴∠M=∠B+
(∠BAO-∠DCO),
∵∠B+∠BAO=∠D+∠DCO,
∴∠BAO-∠DCO=∠D-∠B=38°-32°=6°,
∴∠M=32°+3°=35°;
(3)由(2)可知∠M=∠B+
(∠BAO-∠DCO)=∠B+
(∠D-∠B)=
(∠B+∠D),
∵∠B=α,∠D=β,
∴∠M=
(α+β).
(1)∵∠B=32°,∠A=60°,
∴∠AOB=180°-32°-60°=88°,
∵∠A+∠B=∠C+∠D,
∴∠C=∠A+∠B-∠D=60°+32°-38°=54°;
(2)∵∠M+∠BCM=∠B+∠BAM,
∴∠M=∠B+∠BAM-∠BCM,
∵AM、CM分别平分∠BAO、∠BCD,
∴∠BAM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠M=∠B+
| 1 |
| 2 |
∵∠B+∠BAO=∠D+∠DCO,
∴∠BAO-∠DCO=∠D-∠B=38°-32°=6°,
∴∠M=32°+3°=35°;
(3)由(2)可知∠M=∠B+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠B=α,∠D=β,
∴∠M=
| 1 |
| 2 |
点评:本题主要考查三角形内角和定理及外角的性质,在复杂图形中能充分利用三角形内角和定理及外角的性质找到角之间的关系是解题的关键.

练习册系列答案
相关题目
桌上摆满了朋友们送来的礼物,小狗贝贝好奇地想看个究竟.①小狗先是站在地面上看,②然后抬起了前腿看,③唉,还是站到凳子上看吧,④最后,它终于爬上了桌子…请你根据小狗四次看礼物的顺序,把图乙四副图片按对应字母正确排序为( )
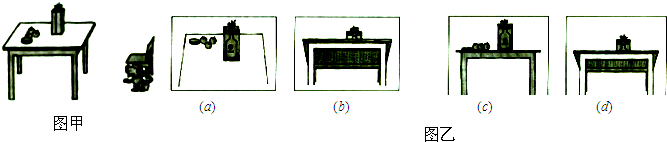

| A、(a) (b) (c) (d) |
| B、(c) (b) (d) (a) |
| C、(b) (a) (c) (d) |
| D、(b) (d) (c) (a) |
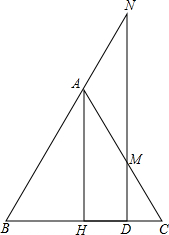 等腰△ABC中,AB=AC,AH⊥BC于H,D是底边上任意一点,过D作BC的垂线交AC于M,交BA的延长线于N,求证:DM+DN=2AH.
等腰△ABC中,AB=AC,AH⊥BC于H,D是底边上任意一点,过D作BC的垂线交AC于M,交BA的延长线于N,求证:DM+DN=2AH. 如图,AC=BC=6cm,∠B=15°,AD⊥BC于点D,则AD的长为
如图,AC=BC=6cm,∠B=15°,AD⊥BC于点D,则AD的长为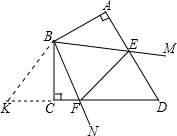 已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=
已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN= 如图所示,⊙O是△ABC的外接圆,
如图所示,⊙O是△ABC的外接圆,
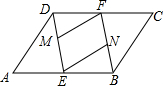 已知在平行四边形ABCD中,AE=CF,点M、N分别是DE、BF的中点,试问ME与FN的数量关系如何?
已知在平行四边形ABCD中,AE=CF,点M、N分别是DE、BF的中点,试问ME与FN的数量关系如何?