题目内容
18.某校为了推进学校均衡发展,计划再购进一批图书,丰富学生的课外阅读.为了解学生对课外阅读的需求情况,学校对学生所喜爱的读物:A.文学,B.艺术,C.科普,D.生活,E.其他,进行了随机抽样调查(规定每名学生只能选其中一类读物),并将调查结果绘制成以下不完整的统计图表.
(1)a=80,b=64,请补全条形统计图;
(2)如果全校有2500名学生,请你估计全校有多少名学生喜爱科普读物;
(3)学校从喜爱科普读物的学生中选拔出2名男生和3名女生,并从中随机抽取2名学生参加科普知识竞赛,请你用树状图或列表法求出恰好抽到一名男生和一名女生的概率.
分析 (1)由E类型的人数及其百分比求得总人数,总人数乘以A类型百分比可得其人数,在用总人数减去其余各组人数得出D类型人数,即可补全条形图;
(2)用总人数乘以样本中C类型所占比例即可得;
(3)用列表法或画树状图法列出所有等可能结果,从中确定恰好抽到一名男生和一名女生的结果数,根据概率公式求解可得.
解答 解:(1)∵抽查的总人数为:32÷10%=320人,
∴a=320×25%=80人,b=320-80-48-96-32=64人;
补全条形统计图如下:
故答案为:80,64;
(2)2500×$\frac{96}{320}$=750人.
答:估计全校喜爱科普读物的学生约有750人.
(3)列表得:
| 女 | 女 | 女 | 男 | 男 | |
| 女 | --- | (女,女) | (女,女) | (男,女) | (男,女) |
| 女 | (女,女) | --- | (女,女) | (男,女) | (男,女) |
| 女 | (女,女) | (女,女) | --- | (男,女) | (男,女) |
| 男 | (女,男) | (女,男) | (女,男) | --- | (男,男) |
| 男 | (女,男) | (女,男) | (女,男) | (男,男) | --- |

所有等可能的情况数有20种,其中一男一女的有12种,
所以P(恰好抽到一男一女)=$\frac{12}{20}=\frac{3}{5}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用以及概率的求法,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
9.若关于x的方程kx2-3x-$\frac{9}{4}$=0有实数根,则实数k的取值范围是( )
| A. | k=0 | B. | k≥-1且k≠0 | C. | k≥-1 | D. | k>-1 |
6.有一个数值转换器,原理如下:当输入的x为64时,输出的y是( )


| A. | $2\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 8 |
3.已知a=-2,则代数式a+1的值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 1 |
10.如图,两个转盘分别自由转动一次,当停止转动时,两个转盘的指针都指向2的概率为( )


| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
7.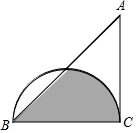 如图,半圆的直径BC恰与等腰直角三角形ABC的一条直角边完全重合.若BC=4,则图中阴影部分的面积是( )
如图,半圆的直径BC恰与等腰直角三角形ABC的一条直角边完全重合.若BC=4,则图中阴影部分的面积是( )
 如图,半圆的直径BC恰与等腰直角三角形ABC的一条直角边完全重合.若BC=4,则图中阴影部分的面积是( )
如图,半圆的直径BC恰与等腰直角三角形ABC的一条直角边完全重合.若BC=4,则图中阴影部分的面积是( )| A. | 2+π | B. | 2+2π | C. | 4+π | D. | 2+4π |