题目内容
5.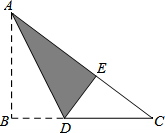 如图,Rt△ABC纸片,∠B=90°,已知BC=8,折叠纸片使边AB落在AC上,点B落在点E处,折痕为AD,且DE=3.求:
如图,Rt△ABC纸片,∠B=90°,已知BC=8,折叠纸片使边AB落在AC上,点B落在点E处,折痕为AD,且DE=3.求:(1)EC的长;
(2)△ABC的面积.
分析 (1)由翻折变换的性质得到BD=DE=3,结合图形求出CD,根据勾股定理求出EC;
(2)设AB=x,由翻折变换的性质得到AE=x,根据勾股定理列出方程,解方程即可.
解答 解:(1)由翻折变换的性质可知,BD=DE=3,
则CD=BC-BD=5,
由勾股定理得,EC=$\sqrt{C{D}^{2}-D{E}^{2}}$=4;
(2)设AB=x,由翻折变换的性质可知,AE=x,
则AC=x+4,
由勾股定理得,AB2+BC2=AC2,
即x2+82=(x+4)2,
解得x=6,
则AB=6,
则△ABC的面积=$\frac{1}{2}$×AB×BC=$\frac{1}{2}$×6×8=24.
点评 本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
13.为了了解某小区居民节约用电情况,物业管理公司随机抽取了今年某一天本小区10户居民的日用电量,数据如表:
(1)求这10户居民的平均日用电量;
(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?
| 用户序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 日用电量(度) | 4.4 | 4.0 | 5.0 | 5.6 | 3.4 | 4.8 | 3.4 | 5.2 | 4.0 | 4.2 |
(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?
14.下列调查中,更适合用普查方式的是( )
| A. | 调查成都电视台《红绿灯》栏目的收视率 | |
| B. | 调查某种灯泡的使用寿命 | |
| C. | 调查成华区居民对“成华精神”的知晓率 | |
| D. | 调查某班学生的体重 |
 如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时分别转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时分别转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y). 如图所示,已知∠1=∠2,∠3=∠4,∠5=∠6,求证:AE∥BD,AD∥BC.
如图所示,已知∠1=∠2,∠3=∠4,∠5=∠6,求证:AE∥BD,AD∥BC.