题目内容
17.已知关于x的一元二次方程x2+mx-m+3=0有两个相等的实数根,求m的值.分析 由于关于x的一元二次方程x2+mx-m+3=0有两个相等的实数根,可知其判别式为0,据此列出关于m的方程,解答即可.
解答 解:∵关于x的一元二次方程x2+mx-m+3=0有两个相等的实数根,
∴m2-4×1×(-m+3)=0,
即m2+4m-12=0,
解之得m1=-6,m2=2,
∴当m=-6或2时,关于x的一元二次方程x2+mx-m+3=0有两个相等的实数根.
点评 本题考查了根的判别式,解题的关键是了解根的判别式如何决定一元二次方程根的情况.

练习册系列答案
相关题目
12.下列说法不正确的是( )
| A. | 一组邻边相等的矩形是正方形 | |
| B. | 对角线互相垂直的平行四边形是菱形 | |
| C. | 等腰梯形的对角和相等 | |
| D. | 矩形的对角线互相垂直平分 |

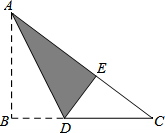 如图,Rt△ABC纸片,∠B=90°,已知BC=8,折叠纸片使边AB落在AC上,点B落在点E处,折痕为AD,且DE=3.求:
如图,Rt△ABC纸片,∠B=90°,已知BC=8,折叠纸片使边AB落在AC上,点B落在点E处,折痕为AD,且DE=3.求: