题目内容
16.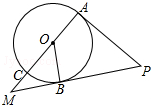 如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.求证:PB是⊙O的切线.
如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.求证:PB是⊙O的切线.
分析 根据切线的性质,可得∠MAP=90°,根据直角三角形的性质,可得∠P+M=90°,根据余角的性质,可得∠M+∠MOB=90°,根据直角三角形的判定,可得∠MOB=90°,根据切线的判定,即可得出结论.
解答 证明:∵PA切⊙O于点A,
∴∠MAP=90°,
∴∠P+M=90°.
∵∠COB=∠APB,
∴∠M+∠MOB=90°,
∴∠MBO=90°,即OB⊥PB,
∵PB经过直径的外端点,
∴PB是⊙O的切线.
点评 本题考查了切线的判定与性质、余角的性质;熟练掌握切线的判定与性质,证出∠MBO=90°是解决问题的关键.

练习册系列答案
相关题目
6.下列说法正确的是( )
| A. | 倒数等于它本身的数只有1 | B. | 相反数等于它本身的数只有1 | ||
| C. | 绝对值等于它本身的数是正数 | D. | 正数的绝对值是它本身 |
7.下列计算正确的是( )
| A. | (π-3)0=1 | B. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{10}$ | C. | (-4)-2=-$\frac{1}{16}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
11.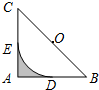 如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
 如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )| A. | $1-\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | $1-\frac{π}{2}$ | D. | $2-\frac{π}{2}$ |
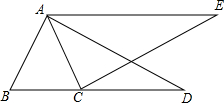 如图,在△ABC中,∠ABC=∠ACB,过A作AD⊥AB交BC的延长线于D,过C作CE⊥AC使AE=BD.求证:∠E=∠D.
如图,在△ABC中,∠ABC=∠ACB,过A作AD⊥AB交BC的延长线于D,过C作CE⊥AC使AE=BD.求证:∠E=∠D.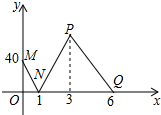 在一条南北方向的航道上依次有A,B,C三个港口,一艘轮船从港口A出发,匀速航行到港口C后返回到港口B,轮船离港口B的距离y(千米)与航行时间x(小时)之间的函数图象如图中的折线MN-NP-PQ所示.已知此次航行过程中水流速度和轮船的静水速度保持不变.
在一条南北方向的航道上依次有A,B,C三个港口,一艘轮船从港口A出发,匀速航行到港口C后返回到港口B,轮船离港口B的距离y(千米)与航行时间x(小时)之间的函数图象如图中的折线MN-NP-PQ所示.已知此次航行过程中水流速度和轮船的静水速度保持不变.