题目内容
11．解方程组：$\left\{\begin{array}{l}{x+y-z=0}\\{x-3y+2z=1}\\{3x+2y-z=4}\end{array}\right.$．分析 用加减消元法或代入法先把三元一次方程组化为二元一次方程组再求解．
解答 解：$\left\{\begin{array}{l}{x+y-z=0①}\\{x-3y+2z=1②}\\{3x+2y-z=4③}\end{array}\right.$，
③-①得：2x+y=4④，
②+③×2得：7x+y=9⑤，
⑤-④得：x=1，
把x=1代入④得：y=2，
把x=1，y=2代入①得：z=3，
所以方程组的解是：$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$．
点评 此题考查三元一次方程组，解三元一次方程组关键是先把三元一次方程组化为二元一次方程组，再用解二元一次方程组的知识求解．
练习册系列答案
阅读快车系列答案
相关题目
1．如图，是测量一物体体积的过程：（1mL=1cm3）
步骤一：将300ml的水装进一个容量为500mL的杯子中；
步骤二：将四颗相同的玻璃球放入水中，结果水没有满；
步骤三：再加一颗同样的玻璃球放入水中，结果水满溢出．
根据以上过程，推测这样一颗玻璃球的体积为下列范围内的（ ）
步骤一：将300ml的水装进一个容量为500mL的杯子中；
步骤二：将四颗相同的玻璃球放入水中，结果水没有满；
步骤三：再加一颗同样的玻璃球放入水中，结果水满溢出．
根据以上过程，推测这样一颗玻璃球的体积为下列范围内的（ ）
| A． | 10cm3以上，20cm3以下 | B． | 20cm3以上，30cm3以下 | ||
| C． | 30cm3以上，40cm3以下 | D． | 40cm3以上，50cm3以下 |
如图所示，直线AB、CD相交于点O，∠DOE：∠BOD=3：2，OF平分∠AOE，若∠AOC=24°，则∠EOF的度数．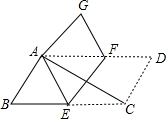
如图，将平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处，