题目内容
8.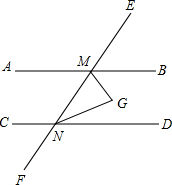 如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,
如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,(1)完成下面的证明:
∵MG平分∠BMN( 已知 ),
∴∠GMN=$\frac{1}{2}$∠BMN( 角平分线的定义 ),
同理∠GNM=$\frac{1}{2}$∠DNM.
∵AB∥CD( 已知 ),
∴∠BMN+∠DNM=180°.
∴∠GMN+∠GNM=90°.
∵∠GMN+∠GNM+∠G=180°( 三角形内角和为180o ),
∴∠G=90°.
∴MG与NG的位置关系是MG⊥NG.
(2)把上面的题设和结论,用文字语言概括为一个命题:两平行直线被第三条直线所截,同旁内角的角平分线互相垂直..
分析 (1)由角平分线的定义和平行线的性质可求得∠GMN+∠GNM=90°,可证得MG⊥NG,根据平行线的性质进行填空即可;
(2)根据MG、NG的特点作出结论.
解答 解:(1)∵MG平分∠BMN(已知)
∴∠GMN=$\frac{1}{2}$∠BMN(角平分线的定义),
同理∠GNM=$\frac{1}{2}$∠DNM.
∵AB∥CD(已知),
∴∠BMN+∠DNM=180°,
∴∠GMN+∠GNM=90°,
∵∠GMN+∠GNM+∠G=180°( 三角形内角和为180o ),
∴∠G=90°,
∴MG与NG的位置关系是MG⊥NG;
故答案为:BMN;DNM;180°;90°;180°;90°;MG⊥NG;
(2)两平行直线被第三条直线所截,同旁内角的角平分线互相垂直.
点评 本题考查了平行线的性质,角平分线的定义,三角形内角和定理,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
16.创建国家森林城市是西安市加强城市生态建设,提升城市品位,构建和谐文明西安的重要举措.在创建国家森林城市过程中,相关部分对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:
栽下的各品种树苗棵树统计表
经观测计算得出丙种树苗的成活率为89.6%.你根据以上信息,解答下列问题:
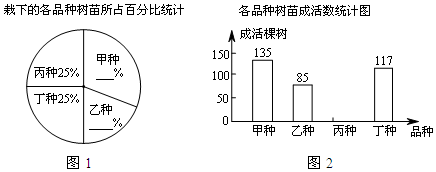
(1)这次栽下的四个品种的树苗共500棵,其中乙品种树苗为100棵;
(2)图1中,甲种树苗占30%,乙种树苗占20%,请将图2补充完整.
栽下的各品种树苗棵树统计表
| 树苗品种 | 甲种 | 乙种 | 丙种 | 丁种 |
| 植树棵树 | 150 | 125 | 125 |

(1)这次栽下的四个品种的树苗共500棵,其中乙品种树苗为100棵;
(2)图1中,甲种树苗占30%,乙种树苗占20%,请将图2补充完整.
18. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
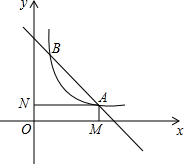 函数y=6-x与函数y=$\frac{4}{x}$交于A、B两点,过点A作x轴与y轴的垂线,垂足分别为M、N,则四边形OMAN的面积和周长分别为多少?
函数y=6-x与函数y=$\frac{4}{x}$交于A、B两点,过点A作x轴与y轴的垂线,垂足分别为M、N,则四边形OMAN的面积和周长分别为多少?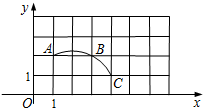 如图,在平面直角坐标系中,过格点A、B、C作一圆弧.
如图,在平面直角坐标系中,过格点A、B、C作一圆弧.