题目内容
4.解方程$\sqrt{\frac{x+4}{x-8}}$-$\sqrt{\frac{x-8}{x+4}}$=$\frac{3}{2}$.分析 设$\sqrt{\frac{x+4}{x-8}}$=y,则$\sqrt{\frac{x-8}{x+4}}$=$\frac{1}{y}$,则原式可化为y-$\frac{1}{y}$=$\frac{3}{2}$,去分母,得2y2-3y-2=0,求得y的值,然后代入$\sqrt{\frac{x+4}{x-8}}$=y,得到关于x的方程求得x的值.
解答 解:设$\sqrt{\frac{x+4}{x-8}}$=y,则$\sqrt{\frac{x-8}{x+4}}$=$\frac{1}{y}$,
则原式可化为y-$\frac{1}{y}$=$\frac{3}{2}$,
去分母,得2y2-3y-2=0.
解得y=2或-$\frac{1}{2}$(舍去).
则$\sqrt{\frac{x+4}{x-8}}$=2,
两边平方得$\frac{x+4}{x-8}$=4,
则x+4=4x-32,
解得:x=12.
经检验x=12是原方程的解
点评 本题考查了无理方程的解法,在解无理方程时最常用的方法是两边平方法及换元法,一般方法是通过观察确定用来换元的式子.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
13.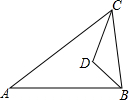 如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D=3∠A,则∠A=( )
如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D=3∠A,则∠A=( )
 如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D=3∠A,则∠A=( )
如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D=3∠A,则∠A=( )| A. | 32° | B. | 36° | C. | 40° | D. | 44° |
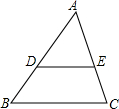 如图,D、E分别在△ABC的边AB、AC上,$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{2}{3}$,且△ABC与△ADE的周长之差为15cm,求△ABC与△ADE的周长.
如图,D、E分别在△ABC的边AB、AC上,$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{2}{3}$,且△ABC与△ADE的周长之差为15cm,求△ABC与△ADE的周长.