题目内容
 如图,在等边三角形ABC中,BD⊥AC于D,延长BC到E,使CE=CD,AB=6cm.
如图,在等边三角形ABC中,BD⊥AC于D,延长BC到E,使CE=CD,AB=6cm.(1)求BE的长;
(2)判断△BDE的形状,并说明理由.
考点:等边三角形的性质,等腰三角形的性质
专题:计算题
分析:(1)根据等边三角形的性质得BC=AB=6cm,再根据“三线合一”得AD=CD=
AC=3cm,而CD=CE=3cm,所以BE=BC+CE=9cm;
(2)根据等边三角形的性质得∠ABC=∠ACB=60°,再根据“三线合一”得∠CBD=
∠ABC=30°,而CD=CE,则∠CDE=∠E,接着利用三角形外角性质得∠CDE+∠E=∠ACB=60°,所以∠E=30°,于是得到∠CBD=∠E,然后根据等腰三角形的判定即可得到△BDE为等腰三角形.
| 1 |
| 2 |
(2)根据等边三角形的性质得∠ABC=∠ACB=60°,再根据“三线合一”得∠CBD=
| 1 |
| 2 |
解答:解:(1)∵△ABC为等边三角形,
∴BC=AB=6cm,
∵BD⊥AC,
∴AD=CD=
AC=3cm,
∵CD=CE=3cm,
∴BE=BC+CE=6cm+3cm=9cm;
(2)△BDE为等腰三角形.理由如下:
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵BD⊥AC,
∴∠CBD=
∠ABC=30°,
∵CD=CE,
∴∠CDE=∠E,
而∠CDE+∠E=∠ACB=60°,
∴∠E=30°,
∴∠CBD=∠E,
∴△BDE为等腰三角形.
∴BC=AB=6cm,
∵BD⊥AC,
∴AD=CD=
| 1 |
| 2 |
∵CD=CE=3cm,
∴BE=BC+CE=6cm+3cm=9cm;
(2)△BDE为等腰三角形.理由如下:
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵BD⊥AC,
∴∠CBD=
| 1 |
| 2 |
∵CD=CE,
∴∠CDE=∠E,
而∠CDE+∠E=∠ACB=60°,
∴∠E=30°,
∴∠CBD=∠E,
∴△BDE为等腰三角形.
点评:本题考查了等边三角形的性质:等边三角形的三个内角都相等,且都等于60°.等边三角形是轴对称图形,它有三条对称轴;它的任意一角的平分线都垂直平分对边,三边的垂直平分线是对称轴.也考查了等腰三角形的判定与性质.

练习册系列答案
相关题目
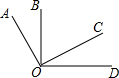 如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )
如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )| A、1个 | B、2个 | C、3个 | D、4个 |
在Rt△ABC中,如果各边的长度都缩小至原来的
,那么锐角A的各个三角函数值( )
| 1 |
| 4 |
A、都缩小
| ||
| B、都扩大4倍 | ||
| C、都不变 | ||
| D、无法确定 |
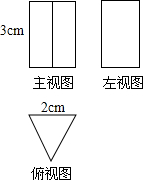 如图是一个几何体从三个方向看所得到的形状图.
如图是一个几何体从三个方向看所得到的形状图.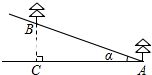 如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求?
如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求? 如图,已知AB与CD相交于O,OE⊥AB,∠EOD=60°,则∠AOC=
如图,已知AB与CD相交于O,OE⊥AB,∠EOD=60°,则∠AOC=