题目内容

19．试说明不论a取何值，方程（a2-2a+2）x2+ax+1=0都是一元二次方程．

分析 要证明无论a取何实数这个方程都是一元二次方程，只要说明无论a为什么值时a2-2a+2的值都不是0，可以利用配方法来证明．

解答 证明：a2-2a+2=（a2-2a+1）+1=（a-1）2+1，
∵（a-1）2≥0，
∴（a-1）2+1≠0，
∴无论a取何实数关于x的方程（a2-2a+2）x2+ax+1=0都是一元二次方程．

点评 本题主要理解配方法，证明一个二次三项式大于或小于0的方法．

练习册系列答案
相关题目
9．如图，正方形ABCD内有两点E、F满足AE=4，EF=FC=12，AE⊥EF，CF⊥EF，则正方形ABCD的边长为10$\sqrt{2}$．
10．有A、B两个黑色袋子，A袋装有3个黑球、2个白球，B袋装有黑、白两个球，这些球除颜色外，其它一样．在随机抽球中，如果从A袋取一个球，再从B袋取一个球，那么得到两个都是黑球的概率是（　　）
A．$\frac{1}{2}$B．$\frac{2}{3}$C．$\frac{1}{5}$D．$\frac{3}{10}$
7．矩形的边长为10和15，其中一个内角平分线分长边为两部分，这两部分的长度分别为（　　）
A．6和9B．5和10C．4和11D．7和8
14．如果x是m，n的比例中项（即x2=m•n），求$\frac{1}{{m}^{2}-{x}^{2}}$+$\frac{1}{{n}^{2}-{x}^{2}}$+$\frac{1}{{x}^{2}}$的值．
4．计算：
（1）$\sqrt{18}$÷$\sqrt{8}$；
（2）$\sqrt{1\frac{2}{3}}$÷$\sqrt{\frac{5}{6}}$；
（3）$\frac{4\sqrt{15}}{2\sqrt{5}}$；
（4）$\frac{2\sqrt{{x}^{2}y}}{3\sqrt{xy}}$；
（5）$\sqrt{\frac{{a}^{2}b}{4{c}^{2}}}$．
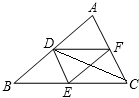11．如图所示，在△ABC中，D，E，F分别为边AB，BC，CA的中点，连接DE，DF，CD，EF，请你判断CD和EF的位置关系，并证明．
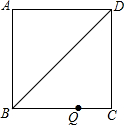7．正方形ABCD的边长为6cm，点Q在边BC上，BQ=2QC．
（1）求BQ的长；
（2）如果点P是对角线BD上的一点，且PQ+PC的值最小，请画图确定P的位置并加以证明；
（3）求PQ+PC的最小值．
8．△ABC三边长分别为2，3，$\sqrt{13}$，则△ABC的面积为3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网