Question

11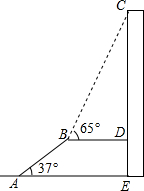．如图，AB是长为10m，倾斜角为37°的自动扶梯，平台BD与大楼CE垂直，且与扶梯AB的长度相等，在B处测得大楼顶部C的仰角为65°，求大楼CE的高度（结果保留整数）．
（参考数据：sin37°≈$\frac{3}{5}$，tan37°≈$\frac{3}{4}$，sin65°≈$\frac{9}{10}$，tan65°≈$\frac{15}{7}$）

Answer 1

分析 作BF⊥AE于点F．则BF=DE，在直角△ABF中利用三角函数求得BF的长，在直角△CDB中利用三角函数求得CD的长，则CE即可求得．

解答 解：作BF⊥AE于点F．则BF=DE．
在直角△ABF中，sin∠BAF=$\frac{BF}{AB}$，则BF=AB•sin∠BAF=10×$\frac{3}{5}$=6（m）．
在直角△CDB中，tan∠CBD=$\frac{CD}{BD}$，则CD=BD•tan65°=10×$\frac{15}{7}$≈21（m）．
则CE=DE+CD=BF+CD=6+21=27（m）．
答：大楼CE的高度是27m．

点评 本题考查了解直角三角形的应用，解答本题关键是构造直角三角形，利用三角函数的知识表示出相关线段的长度．