题目内容
1.已知关于x的不等式组$\left\{\begin{array}{l}4x+2>3(x+a)\\ 2x>3(x-2)+5\end{array}\right.$仅有三个整数解,则a的取值范围是-$\frac{1}{3}$≤a<0.分析 根据解不等式组,可得不等式组的解,根据不等式组的解是整数,可得答案.
解答 解:由4x+2>3x+3a,解得x>3a-2,
由2x>3(x-2)+5,解得3a-2<x<1,
由关于x的不等式组$\left\{\begin{array}{l}4x+2>3(x+a)\\ 2x>3(x-2)+5\end{array}\right.$仅有三个整数解,得-3≤3a-2<-2,
解得-$\frac{1}{3}$≤a<0,
故答案为:-$\frac{1}{3}$≤a<0.
点评 本题考查了一元一次不等式组,利用不等式的解得出关于a的不等式是解题关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
12. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )| A. | 2π | B. | π | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
9.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | (-2a2b)3=-6a6b3 | C. | $\sqrt{8}+\sqrt{2}=3\sqrt{2}$ | D. | (a+b)2=a2+b2 |
13.已知x1,x2是关于x的方程x2+ax-2b=0的两实数根,且x1+x2=-2,x1•x2=1,则ba的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -1 |
19.下列计算中正确的是( )
| A. | x2•x4=x8 | B. | x3+x3=x6 | C. | (-m)2•(-m3)=-m5 | D. | (a3)3=a6 |
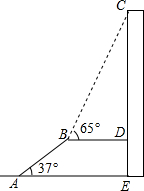 如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).