题目内容
6．
如图，半径为3的⊙O与Rt△AOB的斜边AB切于点D，交OB于点C，连接CD交直线OA于点E，若∠B=30°，则线段AE的长为$\sqrt{3}$．
分析 要求AE的长，只要求出OA和OE的长即可，要求OA的长可以根据∠B=30°和OB的长求得，OE可以根据∠OCE和OC的长求得．
解答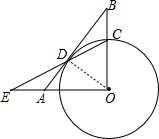 
解：连接OD，如右图所示，
由已知可得，∠BOA=90°，OD=OC=3，∠B=30°，∠ODB=90°，
∴BO=2OD=6，∠BOD=60°，
∴∠ODC=∠OCD=60°，AO=BO•tan30°=$6×\frac{\sqrt{3}}{3}=2\sqrt{3}$，
∵∠COE=90°，OC=3，
∴OE=OC•tan60°=$3×\sqrt{3}=3\sqrt{3}$，
∴AE=OE-OA=$3\sqrt{3}-2\sqrt{3}=\sqrt{3}$，
故答案为：$\sqrt{3}$．
点评 本题考查切线的性质，解题的关键是明确题意，找出所求问题需要的条件．
练习册系列答案
相关题目
16．《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，物品价格为y钱，可列方程组为（ ）
| A． | $\left\{{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{8x+3=y}\\{7x-4=y}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{y-8x=3}\\{y-7x=4}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{8x-y=3}\\{7x-y=4}\end{array}}\right.$ |
17．
如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：
①AD⊥BD；②∠AOC=∠AEC；③BC平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的是（ ）
如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC=∠AEC；③BC平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的是（ ）
| A． | ②④⑤⑥ | B． | ①③⑤⑥ | C． | ②③④⑥ | D． | ①③④⑤ |
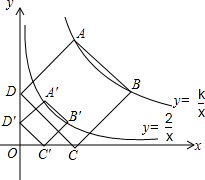如图，正方形ABCD的顶点A，B在函数y=$\frac{k}{x}$（x＞0）的图象上，点C，D分别在x轴，y轴的正半轴上，当k的值改变时，正方形ABCD的大小也随之改变．
1．下列图形：
任取一个是中心对称图形的概率是（ ）
任取一个是中心对称图形的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | 1 |
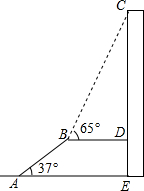如图，AB是长为10m，倾斜角为37°的自动扶梯，平台BD与大楼CE垂直，且与扶梯AB的长度相等，在B处测得大楼顶部C的仰角为65°，求大楼CE的高度（结果保留整数）．
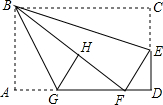如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：
如图，圆柱体中挖去一个小圆柱，那么这个几何体的主视图和俯视图分别为（ ）
