题目内容
16.某果园有100棵橙子树,平均每棵树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x棵橙子树.(1)直接写出平均每棵树结的橙子个数y(个)与x之间的关系;
(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?
分析 (1)根据每多种一棵树,平均每棵树就会少结5个橙子列式即可;
(2)根据题意列出函数解析式,利用配方法把二次函数化为顶点式,根据二次函数的性质进行解答即可.
解答 解:(1)平均每棵树结的橙子个数y(个)与x之间的关系为:y=600-5x(0≤x<120);
(2)设果园多种x棵橙子树时,可使橙子的总产量为w,
则w=(600-5x)(100+x)
=-5x2+100x+60000
=-5(x-10)2+60500,
∵a=-5<0,
∴w的最大值是60500,
则果园多种10棵橙子树时,可使橙子的总产量最大,最大为60500个.
点评 本题考查的是二次函数的应用,根据题意正确列出二次函数解析式、熟练运用配方法、掌握二次函数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.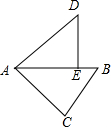 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{5}$ |
5.计算3a2-a2的结果是( )
| A. | 4a2 | B. | 3a2 | C. | 2a2 | D. | 3 |
 P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PA•PB的值称为点P关于⊙O的“幂值”.
P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PA•PB的值称为点P关于⊙O的“幂值”. 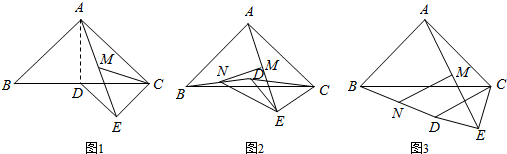
 二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )



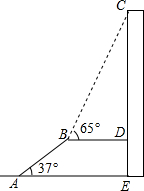 如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).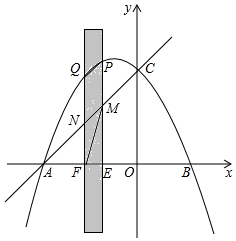 如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.
如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.