题目内容
10.已知二次函数y=2(x-1)2+k的图象上有三点A(-$\sqrt{2}$,y1),B(2,y2),C(5,y3),则y1,y2,y3的大小关系为( )| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y1<y2<y3 |
分析 对二次函数y=2(x-1)2+k,对称轴x=1,在对称轴两侧时,则A、B、C的横坐标离对称轴越近,则纵坐标越小,由此判断y1、y2、y3的大小.
解答 解:在二次函数y=2(x-1)2+k,对称轴x=1,
在图象上的三点A(-$\sqrt{2}$,y1),B(2,y2),C(5,y3),
|5-1|>|-$\sqrt{2}$-1|>|2-1|,
则y1、y2、y3的大小关系为y2<y1<y3.
故选C
点评 本题考查了二次函数图象上点的坐标特征,由点的横坐标到对称轴的距离判断点的纵坐标的大小.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
2.圆内接四边形ABCD中,已知∠A=70°,则∠C等于( )
| A. | 110° | B. | 70° | C. | 30° | D. | 20° |

 如图,AB是⊙O的直径,CD是⊙O的弦,∠DCB=30°,求∠ABD的度数.
如图,AB是⊙O的直径,CD是⊙O的弦,∠DCB=30°,求∠ABD的度数.
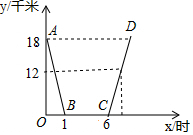 10月2日早晨8点,小华和同学骑自行车去净月潭游玩,当天按原路返回,如图,是小华出行的过程中,他距净月潭的距离y(千米)与他离开家的时间x(小时)之间的函数图象.
10月2日早晨8点,小华和同学骑自行车去净月潭游玩,当天按原路返回,如图,是小华出行的过程中,他距净月潭的距离y(千米)与他离开家的时间x(小时)之间的函数图象.