题目内容
17.先化简,再求值.($\frac{3a}{a-3}$-$\frac{a}{a+3}$)•$\frac{{{a^2}-{9^{\;}}}}{a}$(其中a=2)分析 先根据分式混合运算的法则把原式进行化简,再把a=2代入进行计算即可.
解答 解:原式=$\frac{3a(a+3)-a(a-3)}{(a-3)(a+3)}$•$\frac{{a}^{2}-{9}^{\;}}{a}$
=$\frac{3{a}^{2}+9a-{a}^{2}+3a}{(a-3)(a+3)}$•$\frac{{a}^{2}-{9}^{\;}}{a}$
=$\frac{4{a}^{2}+12a}{(a-3)(a+3)}$•$\frac{{a}^{2}-{9}^{\;}}{a}$
=4a+12,
当a=2时,原式=8+12=20.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
7.已知⊙O的内接正六边形周长为36cm,则这个圆的半径是( )
| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
12.如果|a|=3,|b|=2,且a-b<0.那么a+b的值是( )
| A. | -1,-5 | B. | 1,5 | C. | ±5 | D. | ±1 |
9.方程4x2-8x-25=0的一次项系数和常数项分别为( )
| A. | -2,25 | B. | -2,-25 | C. | 8,-25 | D. | -8,-25 |
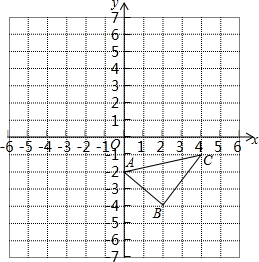 已知:如图,已知△ABC.
已知:如图,已知△ABC.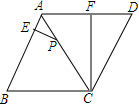 如图,在菱形ABCD中,点P在对角线AC上,且PC=2PA,PE⊥AB于E,CF⊥AD于F,PE=2,求CF的长.
如图,在菱形ABCD中,点P在对角线AC上,且PC=2PA,PE⊥AB于E,CF⊥AD于F,PE=2,求CF的长.