题目内容
8.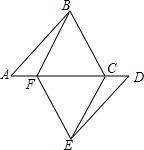 如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.(1)请写出图中两对全等的三角形;
(2)求证:四边形BCEF是平行四边形.
分析 (1)根据SAS可得△ABF≌△DEC,△ABC≌△DEF;
(2)由AB=DE,∠A=∠D,AF=DC,易证得△ABC≌DEF,即可得BC=EF,且BC∥EF,即可判定四边形BCEF是平行四边形;
解答 解:(1)△ABF≌△DEC,△ABC≌△DEF;
(2)证明:∵AF=DC,
∴AF+FC=DC+FC,即AC=DF.
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AC=DF}\\{∠A=∠D}\\{AB=DE}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形.
点评 此题考查了相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质以及勾股定理等知识.此题综合性较强,难度适中,注意数形结合思想的应用.

练习册系列答案
相关题目
1.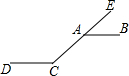 如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )
如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )
 如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )
如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
17.在Rt△ABC中,∠C=90°,∠C的对边为c,∠A的对边为a,则下列关系式中正确的是( )
| A. | c=a•sinA | B. | c=$\frac{a}{sinA}$ | C. | c=a•cosA | D. | c=$\frac{a}{cosA}$ |
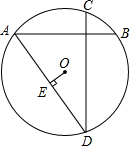 已知AB、CD是⊙O的互相垂直的两条弦,OE⊥AD,垂足为E,求证:OE=$\frac{1}{2}$BC.
已知AB、CD是⊙O的互相垂直的两条弦,OE⊥AD,垂足为E,求证:OE=$\frac{1}{2}$BC.
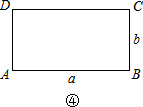 矩形ADQP∽矩形ABCD,那么就称PQ为矩形ABCD的边AB、CD上的相似线.
矩形ADQP∽矩形ABCD,那么就称PQ为矩形ABCD的边AB、CD上的相似线.