题目内容
13.用简便方法计算:$\frac{(199{9}^{2}-2005)(199{9}^{2}+3995)×2000}{1996×1998×2001×2002}$.分析 首先把分子的1999看作2000-1,进一步计算整理,分母分组利用平方差公式和整式的乘法计算方法整理计算,进一步约分得出答案即可.
解答 解:原式=$\frac{(200{0}^{2}-4000+1-2005)(200{0}^{2}-4000+1+3995)×2000}{(2000-4)(2000+1)(2000-2)(2000+2)}$
=$\frac{(200{0}^{2}-6004)(200{0}^{2}-4)×2000}{(200{0}^{2}-4)(200{0}^{2}-6004)}$
=2000.
点评 此题考查因式分解的实际运用,根据数字特点,灵活选用适当的方法解决问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
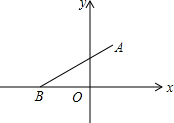 如图,在平面直角坐标系中,点A的坐标为(1,$\sqrt{3}$),点B在x轴的负半轴上,∠ABO=30°.
如图,在平面直角坐标系中,点A的坐标为(1,$\sqrt{3}$),点B在x轴的负半轴上,∠ABO=30°.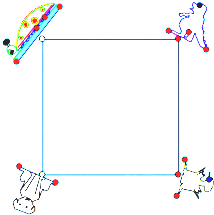 如图,4个小动物分别站在正方形场地的4个顶点,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
如图,4个小动物分别站在正方形场地的4个顶点,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?