题目内容
19．甲、乙两人用两枚质地大小完全相同的正方体做游戏，正方体的每个面上均标有字母A或B，同时抛掷这两枚正方体一次，若朝上的面所标字母相同；否则，乙赢，已知第一枚正方体的六个面所标字母为4个A、2个B．（1）若第二枚正方体的六个面所标字母为2个A、4个B，求甲获胜的概率是多少？
（2）若要使两人获胜概率相等，则第二枚正方体要有个面标记字母A．
分析 （1）用表格列出所有等可能结果，利用概率公式求解可得；
（2）利用表格由概率公式可知，第二枚正方体要有3个面标记字母A．
解答 解：（1）用表格列出所有可能出现的结果：
| A | A | B | B | B | B | |
| A | （A、A） | （A、A） | （A、B） | （A、B） | （A、B） | （A、B） |
| A | （A、A） | （A、A） | （A、B） | （A、B） | （A、B） | （A、B） |
| A | （A、A） | （A、A） | （A、B） | （A、B） | （A、B） | （A、B） |
| A | （A、A） | （A、A） | （A、B） | （A、B） | （A、B） | （A、B） |
| B | （B、A） | （B、A） | （B、B） | （B、B） | （B、B） | （B、B） |
| B | （B、A） | （B、A） | （B、B） | （B、B） | （B、B） | （B、B） |
“两颗骰子的顶面字母相同”记为事件M，它的发生有16种可能，P（M）=$\frac{4}{9}$，
“两颗骰子的顶面字母不同”记为事件N，它的发生有20种可能，P（N）=$\frac{5}{9}$，
∴甲、乙两人获胜的概率各是$\frac{4}{9}$、$\frac{5}{9}$．
（2）若要使两人获胜概率相等，则第二枚正方体要有3个面标记字母A．
| A | A | A | B | B | B | |
| A | （A、A） | （A、A） | （A、A） | （A、B） | （A、B） | （A、B） |
| A | （A、A） | （A、A） | （A、A） | （A、B） | （A、B） | （A、B） |
| A | （A、A） | （A、A） | （A、A） | （A、B） | （A、B） | （A、B） |
| A | （A、A） | （A、A） | （A、A） | （A、B） | （A、B） | （A、B） |
| B | （B、A） | （B、A） | （B、A） | （B、B） | （B、B） | （B、B） |
| B | （B、A） | （B、A） | （B、A） | （B、B） | （B、B） | （B、B） |
点评 此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
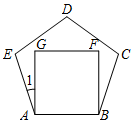如图放置的一个正五边形ABCDE和正方形ABFG边长相等，则∠1=18度．
如图，在四边形ABCD中，AB∥DC，E是CB的中点，AE的延长线与DC的延长线相交于点F．