题目内容
1．
如图，是由7个完全相同的小正方体组成的几何体．则下列4个平面图形中，不是这个几何体的三视图的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据三视图的定义求解即可．
解答 解：A、是作视图，C是主视图，D是俯视图，
故选：B．
点评 本题考查了简单组合体的三视图，熟记三视图是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
11．一手机经销商计划购进某品牌的A型、B型两款手机共40部，每款手机至少要购进10部，设购进A型手机x部，B型手机y部，两款手机的金价和预售价如表：
（1）求出y与x之间的函数关系式；
（3）假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元．
①求出预估利润P（元）与x（部）的函数关系式；
②求出预估利润的最大值，并写出此时购进两款手机各多少部．
| 手机型号 | A型 | B型 |
| 进价（单位：元/部） | 900 | 1200 |
| 预售价（单位：元/部） | 1200 | 1600 |
（3）假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元．
①求出预估利润P（元）与x（部）的函数关系式；
②求出预估利润的最大值，并写出此时购进两款手机各多少部．
9．
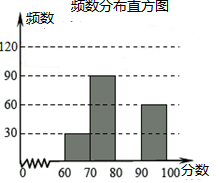某校举行了”文明河南中小学生知识竞赛“活动，并随即抽查了部分同学的成绩，整理并制作成图表如下：
请根据以上图表提供的信息，解答下列问题：
（1）请求出：m=120，n=0.3，抽查的总人数为300人；
（2）请补全频数分布直方图；
（3）抽查成绩的中位数应落在80≤x＜90分数段内；
（4）如果比赛成绩在80分以上（含80分）为优秀，任意抽取一位同学，则成绩优秀的概率为多少？
某校举行了”文明河南中小学生知识竞赛“活动，并随即抽查了部分同学的成绩，整理并制作成图表如下：| 分数段 | 频数 | 频率 |
| 60≤x＜70 | 30 | 0.1 |
| 70≤x＜80 | 90 | n |
| 80≤x＜90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
（1）请求出：m=120，n=0.3，抽查的总人数为300人；
（2）请补全频数分布直方图；
（3）抽查成绩的中位数应落在80≤x＜90分数段内；
（4）如果比赛成绩在80分以上（含80分）为优秀，任意抽取一位同学，则成绩优秀的概率为多少？
16．
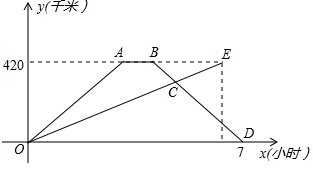快车与慢车分别从相距420千米的甲乙两地同时相向出发，匀速而行，快车到达乙地后停留1小时，然后按原路原速返回，快车比慢车晚1小时到达甲地，快慢两车距各自出发地的路程y（千米）与所用的时间x（时）的关系如图所示，下列说法错误的是（ ）
快车与慢车分别从相距420千米的甲乙两地同时相向出发，匀速而行，快车到达乙地后停留1小时，然后按原路原速返回，快车比慢车晚1小时到达甲地，快慢两车距各自出发地的路程y（千米）与所用的时间x（时）的关系如图所示，下列说法错误的是（ ）| A． | 快车返回的速度为140千米/时 | |
| B． | 慢车的速度为70千米/时 | |
| C． | 快慢两车出发4$\frac{1}{2}$小时时两车相遇 | |
| D． | 出发$\frac{14}{3}$小时时，快慢两车距各自出发地的路程相等 |
13．
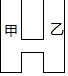如图，某工厂有甲、乙两个大小相同的蓄水池，且中间有管道连通，现要向甲池中注水，若单位时间内的注水量不变，那么从注水开始，乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是（ ）
如图，某工厂有甲、乙两个大小相同的蓄水池，且中间有管道连通，现要向甲池中注水，若单位时间内的注水量不变，那么从注水开始，乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是（ ）| A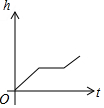． |  | B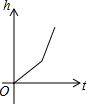． |  | C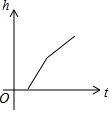． |  | D． |  |
10．
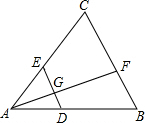如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，点F为BC边上一点，连接AF交DE于点G，则下列结论中一定正确的是（ ）
如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，点F为BC边上一点，连接AF交DE于点G，则下列结论中一定正确的是（ ）| A． | $\frac{AD}{AB}$=$\frac{AE}{EC}$ | B． | $\frac{AG}{GF}$=$\frac{AE}{BD}$ | C． | $\frac{BD}{AD}$=$\frac{CE}{AE}$ | D． | $\frac{AG}{AF}$=$\frac{AC}{EC}$ |