题目内容
16.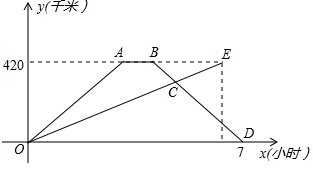 快车与慢车分别从相距420千米的甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快慢两车距各自出发地的路程y(千米)与所用的时间x(时)的关系如图所示,下列说法错误的是( )
快车与慢车分别从相距420千米的甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快慢两车距各自出发地的路程y(千米)与所用的时间x(时)的关系如图所示,下列说法错误的是( )| A. | 快车返回的速度为140千米/时 | |
| B. | 慢车的速度为70千米/时 | |
| C. | 快慢两车出发4$\frac{1}{2}$小时时两车相遇 | |
| D. | 出发$\frac{14}{3}$小时时,快慢两车距各自出发地的路程相等 |
分析 根据题意,快车往返行驶的时间与慢车驶往甲地的时间相同,再根据速度=路程÷时间分别求出两车的速度即可;然后分别求出x=$\frac{14}{3}$和$\frac{9}{2}$时两车行驶的路程,再判断即可.
解答 解:∵快车到达乙地后停留1小时,快车比慢车晚1小时到达甲地,
∴快车往返行驶的时间与慢车驶往甲地的时间相同都是6,
A、快车的速度=$\frac{420×2}{7-1}$=140千米/时,故A正确;
B、慢车的速度=$\frac{420}{7-1}$=70千米/时,故B正确;
C、慢车的解析式为y=70x,当x=$\frac{9}{2}$时,y=315,慢车4$\frac{1}{2}$时离甲地315千米;
快车返回时的解析式为y=-140x+980,当x=$\frac{9}{2}$时,y=350,快车离甲地350千米,
当x=$\frac{9}{2}$时,甲乙已经相遇,故C不符合题意;
D、x=$\frac{14}{3}$时,快车到达乙地又返回,行驶路程=($\frac{14}{3}$-1)×140=$\frac{1540}{3}$千米,
慢车路程=$\frac{14}{3}$×70=$\frac{980}{3}$千米,
∵420×2-$\frac{1540}{3}$=$\frac{980}{3}$千米,
∴快慢两车距各自出发地的路程相等,故D正确;
故选:C.
点评 本题考查了一次函数的应用,主要是行程问题的考查,读懂题目信息以及函数图象表示的行驶过程是解题的关键,难点在于出发$\frac{14}{3}$小时时快车到达乙地并且休息后已经返回.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
7. 圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
 圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )| A. | 12π | B. | 15π | C. | 24π | D. | 30π |
5.抛物线y=-$\frac{3}{5}$(x+$\frac{1}{2}$)2-3的顶点坐标是( )
| A. | ($\frac{1}{2}$,-3) | B. | (-$\frac{1}{2}$,-3) | C. | ($\frac{1}{2}$,3) | D. | (-$\frac{1}{2}$,3) |
6.有一个数值转换器,原理如下:当输入的x为64时,输出的y是( )


| A. | $2\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 8 |
 已知在平面直角坐标系xOy中(如图),已知抛物线y=-x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
已知在平面直角坐标系xOy中(如图),已知抛物线y=-x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.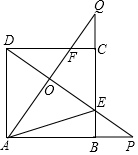 如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=$\frac{13}{16}$,其中正确结论的个数是( )
如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=$\frac{13}{16}$,其中正确结论的个数是( ) 如图,是由7个完全相同的小正方体组成的几何体.则下列4个平面图形中,不是这个几何体的三视图的是( )
如图,是由7个完全相同的小正方体组成的几何体.则下列4个平面图形中,不是这个几何体的三视图的是( )


