题目内容
10.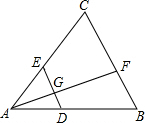 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{EC}$ | B. | $\frac{AG}{GF}$=$\frac{AE}{BD}$ | C. | $\frac{BD}{AD}$=$\frac{CE}{AE}$ | D. | $\frac{AG}{AF}$=$\frac{AC}{EC}$ |
分析 根据相似三角形的判定与性质即可求出答案.
解答 解:(A)∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{AE}{AC}$,故A错误;
(B)∵DE∥BC,
∴$\frac{AG}{GF}=\frac{AE}{EC}$,故B错误;
(C)∵DE∥BC,
$\frac{BD}{AD}=\frac{CE}{AE}$,故C正确;
(D)∵DE∥BC,
∴△AGE∽△AFC,
∴$\frac{AG}{AF}$=$\frac{AE}{AC}$,故D错误;
故选:C.
点评 本题考查相似三角形的判定与性质,解题的关键是熟练运用相似三角形的性质,本题属于中等题型

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.抛物线y=-$\frac{3}{5}$(x+$\frac{1}{2}$)2-3的顶点坐标是( )
| A. | ($\frac{1}{2}$,-3) | B. | (-$\frac{1}{2}$,-3) | C. | ($\frac{1}{2}$,3) | D. | (-$\frac{1}{2}$,3) |
20.-$\frac{2}{3}$的相反数是( )
| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
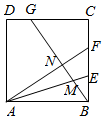 如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=$\frac{4}{3}$NF;③$\frac{BM}{MG}$=$\frac{3}{8}$;④S四边形CGNF=$\frac{1}{2}$S四边形ANGD.其中正确的结论的序号是①③.
如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=$\frac{4}{3}$NF;③$\frac{BM}{MG}$=$\frac{3}{8}$;④S四边形CGNF=$\frac{1}{2}$S四边形ANGD.其中正确的结论的序号是①③. 如图,是由7个完全相同的小正方体组成的几何体.则下列4个平面图形中,不是这个几何体的三视图的是( )
如图,是由7个完全相同的小正方体组成的几何体.则下列4个平面图形中,不是这个几何体的三视图的是( )



 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
 如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.