题目内容
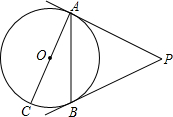如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径且AC=6，∠P=50°，求 |
| BC |
考点：切线的性质,弧长的计算
专题：
分析：连接OB，在四边形AOBP中可求得∠AOB=130°，可得∠BOC=50°，再由AC=6可求得半径，利用弧长计算公式可求得．
解答：
解：连接OB，
∵PA、PB是⊙O的切线，
∴∠OAP=∠OBP=90°，且∠P=50°，
∴∠AOB=360°-90°-90°-50°=130°，
∴∠BOC=50°，
∵AC=6，
∴OC=3，
∴
的长=
=
．
解：连接OB，∵PA、PB是⊙O的切线，
∴∠OAP=∠OBP=90°，且∠P=50°，
∴∠AOB=360°-90°-90°-50°=130°，
∴∠BOC=50°，
∵AC=6，
∴OC=3，
∴
|
| BC |
| 50π•OC |
| 180 |
| 5π |
| 6 |
点评：本题主要考查切线的性质，利用条件求得∠BOC=50°是解题的关键．
练习册系列答案
相关题目
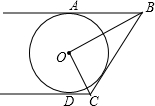如图，已知AB、CD是⊙O的两条平行切线，A、D为切点，∠BOC=90°．求证：BC是⊙O的切线．