题目内容
 如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为
如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为考点:垂径定理,等腰直角三角形,圆周角定理
专题:
分析:根据圆周角定理得∠BOC=2∠A=45°,由于⊙O的直径AB垂直于弦CD,根据垂径定理得CE=DE,且可判断△OCE为等腰直角三角形,所以CE=
OC=2
,然后利用CD=2CE进行计算.
| ||
| 2 |
| 2 |
解答:解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=
OC=2
,
∴CD=2CE=4
.
故答案为4
.
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=
| ||
| 2 |
| 2 |
∴CD=2CE=4
| 2 |
故答案为4
| 2 |
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰直角三角形的性质和圆周角定理.

练习册系列答案
相关题目
 如图,若A是数a在数轴上对应的点,则关于a,0,1的大小关系表示正确的是( )
如图,若A是数a在数轴上对应的点,则关于a,0,1的大小关系表示正确的是( )| A、1<0<a |
| B、a<0<1 |
| C、0<1<a |
| D、0<a<1 |
在
与
之间,无理数的个数有( )
| 3 |
| 27 |
| A、3个 | B、9个 |
| C、27个 | D、无数个 |
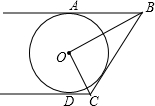 如图,已知AB、CD是⊙O的两条平行切线,A、D为切点,∠BOC=90°.求证:BC是⊙O的切线.
如图,已知AB、CD是⊙O的两条平行切线,A、D为切点,∠BOC=90°.求证:BC是⊙O的切线. 如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.
如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.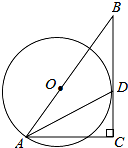 如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,延长BO交⊙O于点A,点D为⊙O上一点,过点A作直线BD的垂线,垂足为C,AD平分∠BAC.
如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,延长BO交⊙O于点A,点D为⊙O上一点,过点A作直线BD的垂线,垂足为C,AD平分∠BAC.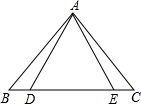 如图,△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于
如图,△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于