题目内容
12.解不等式(组),并把解集在数轴上表示出来.(1)$\frac{x-3}{4}$<6-$\frac{3-4x}{2}$
(2)$\left\{\begin{array}{l}{-3(x-2)>4-x}\\{\frac{1+2x}{3}>1-2x}\end{array}\right.$.
分析 (1)首先两边同时乘以4去分母,然后去括号、移项、合并同类项,最后把x的系数化为1即可;
(2)分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可.
解答 解:(1)x-3<24-2(3-4x),
x-3<24-6+8x,
x-8x<24-6+3,
-7x<21,
x>-3;
(2)$\left\{\begin{array}{l}{-3(x-2)>4-x①}\\{\frac{1+2x}{3}>1-2x②}\end{array}\right.$,
由①得:x<1,
由②得:x>$\frac{1}{4}$,
不等式组的解集为:$\frac{1}{4}$<x<1.
点评 此题主要考查了解一元一次不等式(组),关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
4.在下列多项式乘法运算中,不能运用平方差公式进行运算的是( )
| A. | (2x+3y) (-2x+3y) | B. | (a-2b) (a+2b) | C. | (-x-2y) (x+2y) | D. | (-2x-3y) (3y-2x) |
2.计算x3•x2的结果为( )
| A. | 3x | B. | 2x3 | C. | x6 | D. | x5 |
 如图,BC⊥AE,DE⊥AC,垂足分别为点B,D,BC与DE交于点F,CF=EF,求证:∠DAF=∠BAF.
如图,BC⊥AE,DE⊥AC,垂足分别为点B,D,BC与DE交于点F,CF=EF,求证:∠DAF=∠BAF.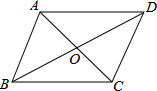 如图,在?ABCD中,对角线AC与BD相交于点O,请添加一个条件AB=AD,使?ABCD成为菱形(写出符合题意的一个条件即可)
如图,在?ABCD中,对角线AC与BD相交于点O,请添加一个条件AB=AD,使?ABCD成为菱形(写出符合题意的一个条件即可)