题目内容
20. 如图,BC⊥AE,DE⊥AC,垂足分别为点B,D,BC与DE交于点F,CF=EF,求证:∠DAF=∠BAF.
如图,BC⊥AE,DE⊥AC,垂足分别为点B,D,BC与DE交于点F,CF=EF,求证:∠DAF=∠BAF.
分析 由全等三角形的判定方法易证△CDF≌△EBF,由全等三角形的性质可得:DF=BF,又因为BC⊥AE,DE⊥AC,所以AF是∠DAB的角平分线,进而可得∠DAF=∠BAF.
解答 证明:∵BC⊥AE,DE⊥AC,
∴∠CDF=∠FBE=90°,
在△CDF和△EBF中
$\left\{\begin{array}{l}{∠CDF=∠EBF=90°}\\{∠DFC=∠BFE}\\{CF=EF}\end{array}\right.$,
∴△CDF≌△EBF(AAS),
∴DF=BF,
又∵BC⊥AE,DE⊥AC,
∴AF是∠DAB的角平分线,
∴∠DAF=∠BAF.
点评 本题考查了全等三角形的判定和性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 在某项针对18-35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如下:
在某项针对18-35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如下:
青年人日均发微信条数统计表
请你根据以上信息解答下列问题:
(1)在表中:a=0.1,b=60;
(2)补全频数分布直方图;
(3)若北京市常住人口中18~35岁的青年人大约有530万人,试估计其中“日均发微信条数”不少于10条的大约有多少万人.
 在某项针对18-35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如下:
在某项针对18-35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微信条数统计表
| m | 频数 | 百分数 |
| A级(0≤m<5) | 90 | 0.3 |
| B级(5≤m<10) | 120 | 0.4 |
| C级(10≤m<15) | b | 0.2 |
| D级(15≤m<20) | 30 | a |
(1)在表中:a=0.1,b=60;
(2)补全频数分布直方图;
(3)若北京市常住人口中18~35岁的青年人大约有530万人,试估计其中“日均发微信条数”不少于10条的大约有多少万人.
11.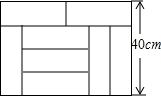 如图,用8块相同的长方形地砖拼成一个大长方形,则每个长方形地砖的面积是( )
如图,用8块相同的长方形地砖拼成一个大长方形,则每个长方形地砖的面积是( )
 如图,用8块相同的长方形地砖拼成一个大长方形,则每个长方形地砖的面积是( )
如图,用8块相同的长方形地砖拼成一个大长方形,则每个长方形地砖的面积是( )| A. | 200cm2 | B. | 300cm2 | C. | 600cm2 | D. | 2400cm2 |
5. 如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10的立方根为( )
如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10的立方根为( )
 如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10的立方根为( )
如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10的立方根为( )| A. | $\sqrt{2}-10$ | B. | -$\sqrt{2}-10$ | C. | 2 | D. | -2 |