题目内容
17.计算:(1)(2x-3y)(3y+2x)
(2)(-x-3y)2
(3)(x+3)2(x-3)2
(4)(a+2b+3)(a+2b-3)
(5)(3x+2y)(2x-3y)-3x(3x-2y)
(6)(-3a4)2-a•a3•a4-a10÷a2.
分析 (1)(3)(4)为了简便计算,可以借助平方差公式进行计算,再进一步合并同类项;
(2)运用完全平方公式进行计算,再进一步合并同类项;
(5)利用整数的乘法计算方法计算;
(6)利用积的乘方和同底数幂的乘方,再计算减法.
解答 解:(1)(2x-3y)(3y+2x)
=(2x-3y)(2x+3y)
=4x2-9y2;
(2)(-x-3y)2
=x2+9y2+6xy;
(3)(x+3)2(x-3)2
=[(x+3)(x-3)]2
=(x-9)2
=x2+81-18x;
(4)(a+2b+3)(a+2b-3)
=(a+2b)2-32
=a2+4b2+4ab-9;
(5)(3x+2y)(2x-3y)-3x(3x-2y)
=6x2-5xy-6y2-9x2+6xy
=-3x2-6y2+xy;
(6)(-3a4)2-a•a3•a4-a10÷a2
=9a8-a8-a8
=7a8.
点评 此题考查整式的混合运算,掌握运算顺序与计算方法是解决问题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
5. 如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10的立方根为( )
如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10的立方根为( )
 如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10的立方根为( )
如图,以原点O为圆心,OB为半径画弧与数轴交于点A,且点A表示的数为x,则x2-10的立方根为( )| A. | $\sqrt{2}-10$ | B. | -$\sqrt{2}-10$ | C. | 2 | D. | -2 |
2.设a、b、c的平均数为M,a、b的平均数为N,N、c的平均数为P,若a>b≥c,则M与P的大小关系是( )
| A. | M<P | B. | M>P | C. | M≥P | D. | 不确定 |
7.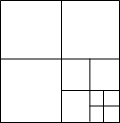 连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
 连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )| A. | ($\frac{1}{2}$)5 | B. | 1-($\frac{1}{4}$)5 | C. | $\frac{1}{5}$ | D. | ($\frac{1}{4}$)5 |
 如图,△ABC∽△A′B′C′,∠C=∠C′=90°,A′B′=2AB,则tanA=tanA′(填“>”、“=”、“<”).
如图,△ABC∽△A′B′C′,∠C=∠C′=90°,A′B′=2AB,则tanA=tanA′(填“>”、“=”、“<”).