题目内容
已知抛物线y=
x2,把它向下平移,得到的抛物线与x轴交于A、B两点,与y轴交于C点.
(1)若△ABC是直角三角形,那么原抛物线应向下平移几个单位?说明理由;
(2)若△ABC是等边三角形,那么原抛物线应向下平移几个单位?说明理由.
| 1 |
| 2 |
(1)若△ABC是直角三角形,那么原抛物线应向下平移几个单位?说明理由;
(2)若△ABC是等边三角形,那么原抛物线应向下平移几个单位?说明理由.
考点:二次函数图象与几何变换
专题:
分析:(1)根据直角三角形的性质,可得OB=OC=OA,根据OB=OC=OA,可得一元二次方程,根据解方程,可得答案;
(2)根据勾股定理,可得BC的长,根据等边三角形的性质,可得方程,根据解方程,可得答案.
(2)根据勾股定理,可得BC的长,根据等边三角形的性质,可得方程,根据解方程,可得答案.
解答:解:(1)若△ABC是直角三角形,那么原抛物线应向下平移2个单位,理由如下:
设向下平移b个单位,若△ABC是直角三角形,
y=
x2-b,
可得A(-
,0)B(
,0)C(0,-b),
△ABC是直角三角形,
OB=OC=OA,
=b,解得b=2,
若△ABC是直角三角形,那么原抛物线应向下平移2个单位;
(2)若△ABC是等边三角形,那么原抛物线应向下平移6个单位,理由如下
设向下平移b个单位,若△ABC是直角三角形,
y=
x2-b,
可得A(-
,0)B(
,0)C(0,-b),
AB=2
,BC=
,
若△ABC是等边三角形,
AB=BC,即2
=
,
解得b=6.
若△ABC是等边三角形,那么原抛物线应向下平移6个单位.
设向下平移b个单位,若△ABC是直角三角形,
y=
| 1 |
| 2 |
可得A(-
| 2b |
| 2b |
△ABC是直角三角形,
OB=OC=OA,
| 2b |
若△ABC是直角三角形,那么原抛物线应向下平移2个单位;
(2)若△ABC是等边三角形,那么原抛物线应向下平移6个单位,理由如下
设向下平移b个单位,若△ABC是直角三角形,
y=
| 1 |
| 2 |
可得A(-
| 2b |
| 2b |
AB=2
| 2b |
| 2b+b2 |
若△ABC是等边三角形,
AB=BC,即2
| 2b |
| 2b+b2 |
解得b=6.
若△ABC是等边三角形,那么原抛物线应向下平移6个单位.
点评:本题考查了二次函数图象与几何变换,利用了直角三角形的性质,等边三角形的性质,函数图象平移的规律.

练习册系列答案
相关题目
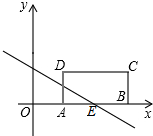 如图所示,在平面直角坐标系中,矩形ABCD的边AB位于x轴,A(1,0),B(3,0),矩形的宽AD为1,一条直线y=kx+2(k≠0)与折线ABC交于点E.
如图所示,在平面直角坐标系中,矩形ABCD的边AB位于x轴,A(1,0),B(3,0),矩形的宽AD为1,一条直线y=kx+2(k≠0)与折线ABC交于点E.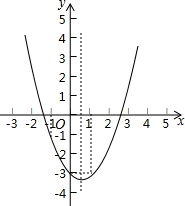 已知抛物线y=ax2+bx+c的图象如图所示,
已知抛物线y=ax2+bx+c的图象如图所示, 在菱形ABCD中,∠ABC=120°,对角线AC、BD交于点O,AE平分∠CAD,分别交OD、CD于F、E两点,求∠AFO的度数.
在菱形ABCD中,∠ABC=120°,对角线AC、BD交于点O,AE平分∠CAD,分别交OD、CD于F、E两点,求∠AFO的度数.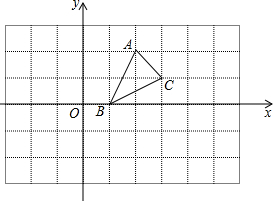 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的三个顶点的坐标分别是:A(2,2),B(1,0),C(3,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的三个顶点的坐标分别是:A(2,2),B(1,0),C(3,1).