题目内容
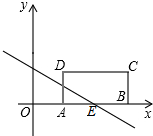 如图所示,在平面直角坐标系中,矩形ABCD的边AB位于x轴,A(1,0),B(3,0),矩形的宽AD为1,一条直线y=kx+2(k≠0)与折线ABC交于点E.
如图所示,在平面直角坐标系中,矩形ABCD的边AB位于x轴,A(1,0),B(3,0),矩形的宽AD为1,一条直线y=kx+2(k≠0)与折线ABC交于点E.(1)证明:直线y=kx+2始终经过一个定点,并写出该定点坐标;
(2)当直线y=kx+2与矩形ABCD有交点时,求k的取值范围;
(3)设△CDE的面积为S,试求S与k的函数解析式.
考点:一次函数综合题
专题:
分析:(1)根据一次函数的图象,不论k取何值,当x=0时,y=2一定成立,据此即可判断;
(2)求得直线经过点A和点C时对应的k的值,即可判断;
(3)分成点E在AB上和BC上两种情况进行讨论,利用三角形的面积公式即可求解.
(2)求得直线经过点A和点C时对应的k的值,即可判断;
(3)分成点E在AB上和BC上两种情况进行讨论,利用三角形的面积公式即可求解.
解答:解:(1)不论k取何值,当x=0时,y=2,则函数一定经过顶点(0,2);
(2)当直线经过点A时,把点(1,0)代入y=kx+2得:k+2=0,解得:k=-2;
当直线经过点C(3,1)时,代入y=kx+2得:3k+2=1,解得:k=-
,
则k的取值范围是:-2≤k≤-
;
(3)CD=3-1=2,
当直线经过点B时,把B的坐标(3,0),代入y=kx+2得:3k+2=0,解得:k=-
,
当-2≤k≤-
时,E在AB上,则S△CDE=
×2×1=1;
当-
<k≤-
时,E在BC上,在y=kx+2中,令x=3,则y=3k+2,则CE=1-(3k+2)=-3k-1
则S△CDE=
×2×(-3k-1)=-3k-1.
即S=-3k-1.
(2)当直线经过点A时,把点(1,0)代入y=kx+2得:k+2=0,解得:k=-2;
当直线经过点C(3,1)时,代入y=kx+2得:3k+2=1,解得:k=-
| 1 |
| 3 |
则k的取值范围是:-2≤k≤-
| 1 |
| 3 |
(3)CD=3-1=2,
当直线经过点B时,把B的坐标(3,0),代入y=kx+2得:3k+2=0,解得:k=-
| 2 |
| 3 |
当-2≤k≤-
| 2 |
| 3 |
| 1 |
| 2 |
当-
| 2 |
| 3 |
| 1 |
| 3 |
则S△CDE=
| 1 |
| 2 |
即S=-3k-1.
点评:本题考查了待定系数法求函数的解析式以及三角形的面积公式,正确确定k的取值范围是关键.

练习册系列答案
相关题目
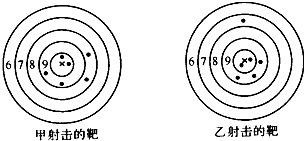 如图是甲,乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.
如图是甲,乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.