题目内容
9．
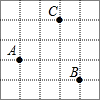如图，已知每个小方格的边长都是1，A，B，C三点都在小方格的顶点上，则AB+BC=2$\sqrt{10}$．
分析 由正方形的性质和勾股定理求出AB、BC，即可得出AB+BC．
解答 解：连接AB、BC，如图所示：
由勾股定理得：AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，BC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，
∴AB+BC=$\sqrt{10}$+$\sqrt{10}$=2$\sqrt{10}$；
故答案为：2$\sqrt{10}$．
点评 本题考查了正方形的性质、勾股定理；熟练掌握勾股定理，运用勾股定理正确计算得出AB和BC是解决问题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
5．
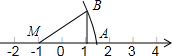如图，MA=MB，则数轴上点A对应的数是（ ）
如图，MA=MB，则数轴上点A对应的数是（ ）| A． | $\sqrt{5}$+1 | B． | -$\sqrt{5}$+1 | C． | -$\sqrt{5}$-1 | D． | $\sqrt{5}$-1 |
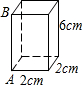如图，长方体的底面是边长为2cm的正方形，高是6cm．