题目内容

5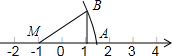．如图，MA=MB，则数轴上点A对应的数是（　　）
A．$\sqrt{5}$+1B．-$\sqrt{5}$+1C．-$\sqrt{5}$-1D．$\sqrt{5}$-1

分析 首先在直角三角形中，利用勾股定理求出线段MB的长度，得出MA的长度，求出点A与原点的距离，即可得出数轴上点A所表示的数．

解答 解：根据题意，由勾股定理得：MB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∵MA=MB，
∴MA=$\sqrt{5}$，
∴A到原点的距离是$\sqrt{5}$-1，
∵A在原点右侧，
∴点A所表示的数是$\sqrt{5}$-1，
故选D．

点评 此题主要考查了实数与数轴之间的对应关系、勾股定理；熟练掌握勾股定理，并能进行推理计算是解决问题的关键．

练习册系列答案
相关题目
16．在-（-5），（-5）2，-|-5|，-52中负数有2个．
17．三条边上的高（高所在直线）的交点在三角形上的是直角三角形．
13．已知两个有理数相加，和小于每一个加数，请写出满足上述条件的一个算式：（-2）+（-3）=-5．
20．直角三角形中，一条直角边长为24cm，斜边长为25cm，则另一直角边长为（　　）
A．7cmB．12cmC．16cmD．49cm
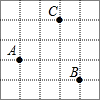9．如图，已知每个小方格的边长都是1，A，B，C三点都在小方格的顶点上，则AB+BC=2$\sqrt{10}$．
16．把下列各数填入相应的集合内：
$\sqrt{12}$，0，$\root{3}{-8}$．-$\frac{1}{6}$，0.2$\stackrel{•}{5}$，-$\frac{π}{3}$，0.3030030003…（相邻两个3之间0的个数逐次加1）．
（1）正实数集合{$\sqrt{12}$，0，0.2$\stackrel{•}{5}$，0.3030030003……}
（2）负实数集合{$\root{3}{-8}$，-$\frac{1}{6}$，-$\frac{π}{3}$…}
（3）有理数集合{0，$\root{3}{-8}$．-$\frac{1}{6}$，0.2$\stackrel{•}{5}$…}
（4）无理数集合{$\sqrt{12}$，-$\frac{π}{3}$，0.3030030003……}．
12．如图，四边形ABCD内接于⊙O，AD、BC的延长线交于点E，点F在BD的延长线上，且DE平分∠CDF．
（1）求证：AB=AC；
（2）找出图中的相似三角形；
（3）若AC=3，AD=2，求DE的长．
13．2015年1月29日网易新闻报道，2014年中国铁路总公司进一步加快铁路建设，各项铁路建设任务全面完成，新线投产8427公顷，创历史最高纪录．某两个城市间铁路新建后，列车行驶的路程比原铁路列车行驶的路程短，新铁路列车每小时的设计运行速度比原铁路列车设计运行速度的2倍还多40千米，这两个列车设计运行速度的乘积为16000．（提示：182=324）
（1）求原铁路的列车设计运行速度；
（2）专家建议，从安全角度考虑，列车实际的运行速度要比设计的运行速度减少m%，以便有充分的时间应对突发事件，这样这两个城市间的实际运行时间比设计运行时间增加$\frac{1}{10}m$小时，若这两个城市间新铁路列车行驶的路程为1600千米，求m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网