题目内容
1.已知△ABC中,∠B比∠A大30°,∠B比∠C小30°,求三角形三个内角的度数.分析 设∠A=x,然后表示出∠B、∠C,再根据三角形的内角和等于180°列方程求解即可.
解答 解:设∠A=x,则∠B=x+30°,∠C=x+30°+30°=x+60°,
由三角形的内角和定理得,∠A+∠B+∠C=180°,
即x+x+30°+x+60°=180°,
解得x=30°,
所以,∠A=30°,∠B=60°,∠C=90°.
点评 本题考查了三角形的内角和定理,是基础题,难点在于用∠A表示出另两个角并列出方程.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.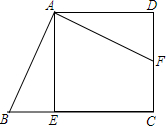 如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
 如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )| A. | DF=EB | B. | AE⊥BC | C. | ∠DAF=∠EAB | D. | AB=AD |
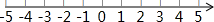 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.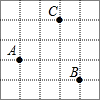 如图,已知每个小方格的边长都是1,A,B,C三点都在小方格的顶点上,则AB+BC=2$\sqrt{10}$.
如图,已知每个小方格的边长都是1,A,B,C三点都在小方格的顶点上,则AB+BC=2$\sqrt{10}$. 某幢建筑物从16m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图),如果抛物线的最高点M离墙1m,离地面18m,则水流落地点B离墙的距离OB是( )
某幢建筑物从16m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图),如果抛物线的最高点M离墙1m,离地面18m,则水流落地点B离墙的距离OB是( )