题目内容
18.先化简,再求值:$\frac{2}{a+1}-\frac{a-2}{{{a^2}-1}}÷\frac{{{a^2}-2a}}{{{a^2}-2a+1}}$,其中a=0.5.分析 原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{2}{a+1}$-$\frac{a-2}{(a+1)(a-1)}$•$\frac{(a-1)^{2}}{a(a-2)}$=$\frac{2}{a+1}$-$\frac{a-1}{a(a+1)}$=$\frac{2a-a+1}{a(a+1)}$=$\frac{1}{a}$,
当a=0.5时,原式=2.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9.纳米是一种长度单位,已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示该种花粉的直径为( )
| A. | 3.5×104米 | B. | 0.35×104米 | C. | 3.5×104纳米 | D. | 35×103纳米 |
3.等腰三角形的腰长为10cm,底边上的高是8cm,则该等腰三角形的周长是( )
| A. | 12cm | B. | 22cm | C. | 26cm | D. | 32cm |
6.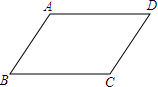 如图,在?ABCD中,∠B=60°,?ABCD的周长为20.若设AB的长度为2x,?ABCD的面积为y,则下列说法中正确的是( )
如图,在?ABCD中,∠B=60°,?ABCD的周长为20.若设AB的长度为2x,?ABCD的面积为y,则下列说法中正确的是( )
 如图,在?ABCD中,∠B=60°,?ABCD的周长为20.若设AB的长度为2x,?ABCD的面积为y,则下列说法中正确的是( )
如图,在?ABCD中,∠B=60°,?ABCD的周长为20.若设AB的长度为2x,?ABCD的面积为y,则下列说法中正确的是( )| A. | y=$\sqrt{3}{x}^{2}$-3$\sqrt{3}$ | B. | 当x=2时,y=15$\sqrt{3}$ | ||
| C. | 当x=$\frac{5}{2}$时,?ABCD的面积取得最大值 | D. | 当x>$\frac{5}{2}$时,y$>\frac{25\sqrt{3}}{2}$ |
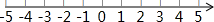 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.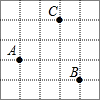 如图,已知每个小方格的边长都是1,A,B,C三点都在小方格的顶点上,则AB+BC=2$\sqrt{10}$.
如图,已知每个小方格的边长都是1,A,B,C三点都在小方格的顶点上,则AB+BC=2$\sqrt{10}$.