题目内容
20.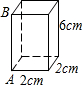 如图,长方体的底面是边长为2cm的正方形,高是6cm.
如图,长方体的底面是边长为2cm的正方形,高是6cm.(1)如果用一根细线从点A开始经过4个侧面围绕一圈到达点B.那么所用的细线最短长度是多少厘米?
(2)如果从A点开始经过4个侧面缠绕2圈到达点B,那么所用细线最短长度是多少厘米?
分析 (1)把长方体沿AB边剪开,再根据勾股定理进行解答即可;
(2)如果从点如果从点A开始经过4个侧面缠绕2圈到达点B,相当于直角三角形的两条直角边分别是8和3,再根据勾股定理求出斜边长即可.
解答  解:(1)如图1所示:
解:(1)如图1所示:
连接AB′,则AB′即为所用的最短细线长,
AA′=8cm,A′B′=AB=6cm,
由勾股定理得:AB′2=AA′2+A′B′2=62+82=100,
则AB′=10cm,
答:所用的细线最短长度是10cm; (2)将长方体的侧面沿AB展开,取A′B′的中点C,连接BC,AC,则AC+BC为所求的最短细线长,
(2)将长方体的侧面沿AB展开,取A′B′的中点C,连接BC,AC,则AC+BC为所求的最短细线长,
AC2=AA′2+A′C′2,AC=$\sqrt{73}$cm,
AC2=BB′2+CB′2=73,
BC=$\sqrt{73}$(cm),
AC+BC=2$\sqrt{73}$(cm),
答:所用细线最短长度是2$\sqrt{73}$cm.
点评 本题考查的是平面展开-最短路线问题,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
13.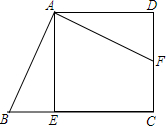 如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
 如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )| A. | DF=EB | B. | AE⊥BC | C. | ∠DAF=∠EAB | D. | AB=AD |
12. 如图,四边形ABCD内接于⊙O,AD、BC的延长线交于点E,点F在BD的延长线上,且DE平分∠CDF.
如图,四边形ABCD内接于⊙O,AD、BC的延长线交于点E,点F在BD的延长线上,且DE平分∠CDF.
(1)求证:AB=AC;
(2)找出图中的相似三角形;
(3)若AC=3,AD=2,求DE的长.
 如图,四边形ABCD内接于⊙O,AD、BC的延长线交于点E,点F在BD的延长线上,且DE平分∠CDF.
如图,四边形ABCD内接于⊙O,AD、BC的延长线交于点E,点F在BD的延长线上,且DE平分∠CDF.(1)求证:AB=AC;
(2)找出图中的相似三角形;
(3)若AC=3,AD=2,求DE的长.
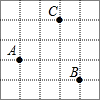 如图,已知每个小方格的边长都是1,A,B,C三点都在小方格的顶点上,则AB+BC=2$\sqrt{10}$.
如图,已知每个小方格的边长都是1,A,B,C三点都在小方格的顶点上,则AB+BC=2$\sqrt{10}$. 某幢建筑物从16m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图),如果抛物线的最高点M离墙1m,离地面18m,则水流落地点B离墙的距离OB是( )
某幢建筑物从16m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图),如果抛物线的最高点M离墙1m,离地面18m,则水流落地点B离墙的距离OB是( )