题目内容
18.(1)解下列不等式:2x+5>10.(2)解下列不等式组,并在数轴上表示解集:$\left\{\begin{array}{l}{x-1≤2}\\{x+1<2}\end{array}\right.$.
分析 (1)不等式移项合并,将x系数化为1,即可求出解集.
(2)分别求出各不等式的解集,再在数轴上表示出来即可.
解答 解:(1)移项合并得:2x>5,
解得:x>$\frac{5}{2}$;
(2)$\left\{\begin{array}{l}{x-1≤2①}\\{x+1<2②}\end{array}\right.$
由①得,x≤3,
由②得,x<1,
故不等式的解集为:x<1,
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
3.已知P1(-1,y1),P2(2,y2)是正比例函数y=-x图象上的两个点,则y1、y2的大小关系是( )
| A. | y1=y2 | B. | y1<y2 | C. | y1>y2 | D. | 不能确定 |
10.下列二元一次方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$的是( )
| A. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-4}\end{array}\right.$ |
 某几何体的三视图及相关数据如图所示.
某几何体的三视图及相关数据如图所示.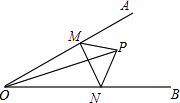 如图,∠AOB=30°,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=8.
如图,∠AOB=30°,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=8.
 如图,已知锐角三角形ABC,求作⊙C,使⊙C与AB所在的直线相切于点D(保留作图痕迹,不写作法).
如图,已知锐角三角形ABC,求作⊙C,使⊙C与AB所在的直线相切于点D(保留作图痕迹,不写作法).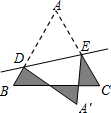 如图,等边△ABC的边长为3cm,D,E分别是边AB,AC上的点,将△ADE沿直线DE折叠,使点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为9cm.
如图,等边△ABC的边长为3cm,D,E分别是边AB,AC上的点,将△ADE沿直线DE折叠,使点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为9cm.