题目内容
 如图△ABC中,∠A=62°,∠ACD=35°,∠ABE=20°,则∠BFD的度数是
如图△ABC中,∠A=62°,∠ACD=35°,∠ABE=20°,则∠BFD的度数是考点:三角形内角和定理
专题:
分析:在△ABC中结合条件可求得∠FBC+∠FCB,在△BCF中利用外角的性质可求得∠BFD的大小.
解答:解:∵∠A+∠ABC+∠ACB=180°,
∴∠FBC+∠FCB=180°-∠A-∠ABE-∠ACD=180°-62°-20°-35°=63°,
∵在△BCF中,∠BFD为△BCF的外角,
∴∠BFD=∠FBC+∠FCB=63°,
故答案为:63°.
∴∠FBC+∠FCB=180°-∠A-∠ABE-∠ACD=180°-62°-20°-35°=63°,
∵在△BCF中,∠BFD为△BCF的外角,
∴∠BFD=∠FBC+∠FCB=63°,
故答案为:63°.
点评:本题主要考查三角形内角和定理和外角的性质,求得∠FBC+∠FCB是解题的关键,解决这类问题时注意三角形内角和为180°这一隐含条件.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
下列代数式中,全是单项式的一组是( )
A、3x,x-
| ||||||
B、
| ||||||
C、
| ||||||
| D、x+y,xyz,3z |
下列各式中,正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若关于x的多项式x2-2(m-3)x+16是完全平方式,则m的值为( )
| A、±7 | B、±1 |
| C、1或-7 | D、-1或7 |
如果
x2-3x=1是关于x的一元一次方程,则a的值是( )
| 9-2a |
| 3 |
| A、0 | B、3 | C、4.5 | D、4 |
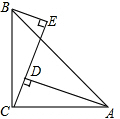 如图,∠E=∠CDA=∠ACB=90°,AC=BC.试猜想BE、AD、DE的数量关系?试加以证明.
如图,∠E=∠CDA=∠ACB=90°,AC=BC.试猜想BE、AD、DE的数量关系?试加以证明. 如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点. 已知直线y=
已知直线y=