题目内容
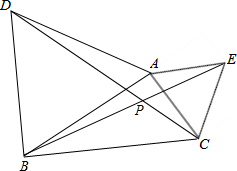 如图,△ABD,△AEC都是等边三角形.设BE,DC交于点P,连接AP,求式子
如图,△ABD,△AEC都是等边三角形.设BE,DC交于点P,连接AP,求式子| PB+PC+2PA |
| PD+PE |
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:在DP上截取DG=PB,连接AG,AP,易证△CAD≌△EAB,可得∠ADC=∠ABE,∠AEB=∠ACD,即可证明△ADG≌△ABP,可得∠DAG=∠BAP,AG=AP,即可判定△PAG为等边三角形,易得∠CAG=∠EAP,即可证明△CAG≌△EAP,可得CG=PE,即可解题.
解答:解:在DP上截取DG=PB,连接AG,AP,

∵△ABD、△AEC等边三角形,
∴∠BAD=∠CAE=60°,AC=AE,AD=AB,
∴∠BAD+∠BAC=∠BAC+∠CAE,即∠BAE=∠CAD,
在△CAD和△EAB中,
,
∴△CAD≌△EAB(SAS),
∴∠ADC=∠ABE,∠AEB=∠ACD,
在△ADG和△ABP中,
,
∴△ADG≌△ABP(SAS),
∴∠DAG=∠BAP,AG=AP,
∵∠DAG+∠BAG=60°,∴∠BAG+∠BAP=60°,即∠PAG=60°,
∴△PAG为等边三角形,∠PAG+∠CAP=∠CAP+∠CAE,即∠CAG=∠EAP,
∴PA=PG,
在△CAG和△EAP中,
,
∴△CAG≌△EAP(SAS),
∴CG=PE,
∴PD+PE=DG+PG+PC+PG=PB+PC+2PA,
∴
=1.

∵△ABD、△AEC等边三角形,
∴∠BAD=∠CAE=60°,AC=AE,AD=AB,
∴∠BAD+∠BAC=∠BAC+∠CAE,即∠BAE=∠CAD,
在△CAD和△EAB中,
|
∴△CAD≌△EAB(SAS),
∴∠ADC=∠ABE,∠AEB=∠ACD,
在△ADG和△ABP中,
|
∴△ADG≌△ABP(SAS),
∴∠DAG=∠BAP,AG=AP,
∵∠DAG+∠BAG=60°,∴∠BAG+∠BAP=60°,即∠PAG=60°,
∴△PAG为等边三角形,∠PAG+∠CAP=∠CAP+∠CAE,即∠CAG=∠EAP,
∴PA=PG,
在△CAG和△EAP中,
|
∴△CAG≌△EAP(SAS),
∴CG=PE,
∴PD+PE=DG+PG+PC+PG=PB+PC+2PA,
∴
| PB+PC+2PA |
| PD+PE |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△CAD≌△EAB、△ADG≌△ABP和△CAG≌△EAP是解题的关键.

练习册系列答案
相关题目
若关于x的多项式x2-2(m-3)x+16是完全平方式,则m的值为( )
| A、±7 | B、±1 |
| C、1或-7 | D、-1或7 |
如果
x2-3x=1是关于x的一元一次方程,则a的值是( )
| 9-2a |
| 3 |
| A、0 | B、3 | C、4.5 | D、4 |
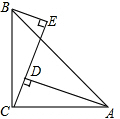 如图,∠E=∠CDA=∠ACB=90°,AC=BC.试猜想BE、AD、DE的数量关系?试加以证明.
如图,∠E=∠CDA=∠ACB=90°,AC=BC.试猜想BE、AD、DE的数量关系?试加以证明. 已知直线y=
已知直线y=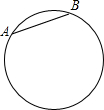 如图是挂在墙上的一面大镜子,上面有两点A、B.小明想知道A、B两点之间的距离,但镜子挂得太高,他只能够到镜子的一部分,无法直接测量,旁边又没有梯子,只有一根长度比圆的直径稍长点的竹竿和一把尺子,你能帮助小明完成吗?若能,请写出测量步骤,并说明理由.
如图是挂在墙上的一面大镜子,上面有两点A、B.小明想知道A、B两点之间的距离,但镜子挂得太高,他只能够到镜子的一部分,无法直接测量,旁边又没有梯子,只有一根长度比圆的直径稍长点的竹竿和一把尺子,你能帮助小明完成吗?若能,请写出测量步骤,并说明理由.